戾換法

戾換法(method of distorted replacement)是以性質判斷為前提，對該前提連續互動套用換質法和換位法，從而得出結論，而該結論的主項必須是前提主項的矛盾概念。例如：“所有的商品都是勞動產品”(前提)，經過換質得出“所有的商品都不是非勞動產品”，再進行換位得出“非勞動產品不是商品”，再換質得出“非勞動產品是非商品”，再換位得出“有些非商品是非勞動產品”。戾換法是換質法和換位法的綜合運用，它沒有特殊規則，運用時遵守換質、換位規則。戾換法分為兩種：不完全戾換和完全戾換。運用戾換法時，必須假定原判斷的主項、謂項所反映的對象實際存在。

基本介紹

• 中文名：戾換法
• 外文名：inversion;method of distorted replacement
• 規則：換質法和換位法的規則
• 分類：不完全戾換和完全戾換

基本介紹

戾換法是這樣一種直接推理：前提的主項是“S”，結論的主項是“非S”。先將全稱肯定命題“凡S是P”換質為“無S是非P”，再換位為“沒有非P是S”，再換質為“凡非P是非S”，再換位為“有非S是非P”，最後還可換質得“有非S不是P”。整個推理過程都遵循換位法和換質法的規則。例如從“凡偶數是整數”可用戾換法得到“有非偶數是非整數”，“有非偶數不是整數”。

相關說明

全稱否定命題“無S是P”換位得“無P是S”，換質又得“凡P不是非S”，再換位得“有非S不是P”，最後還可換質得“有非S是非嚴”。例如從“無奇數是偶數”經戾換得“有非奇數不是偶數”，“有非奇數是非偶數”。

特稱命題顯然不能進行戾換法推理。

我們可以用下表來表示戾換法的有效推理形式：

前 提	結論
A：凡S是P	I：有非S是非P O：有非S不是P
E：無S是P	O：有非S不是P I：有非S是非P
I：有S是P	不能得結論
O：有S不是P	不能得結論

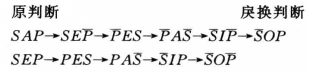
從規則方面看，戾換法並不包含什麼新的原則。但是戾換法從SA 推出OP(“”是“非S”的簡寫，“P”是“非P”的簡寫)，而“P”在SAP中不周延，卻在OP中周延，這就違反了在前提中不周延的概念，在結論中也不周延這條規則。這裡暴露了傳統邏輯的毛病。產生這個毛病的根本原因在於傳統邏輯既不考慮到全類，又不考慮到空類。在討論直言命題，直接推理以至三段論時，所涉及的類都是非空非全的。

從SAP戾換得到OP要求 存在，即有事物不是P。這就是說P不是全類，也就是說不是空類。“P”在OP中周延，來自“P”在隱含的前提“有事物不是P”中周延。

從SAP戾換得到OP，是從全稱命題過渡到特稱命題。這就要求存在，如果 是空類，或者說如果S是全類OP就不真。例如“凡發展的事物都有內部矛盾”戾換得到的“有不發展的事物沒有內部矛盾”是假的，因為不發展的事物是不存在的。

傳統邏輯並不懷疑SAP可推出SIP。其實當S是空類時，這樣的推理不是有效的。例如從“任何未接觸過細菌的人都不會得細菌性傳染病”推不出“有未接觸過細菌的人不會得細菌性傳染病”。

現代邏輯認為傳統邏輯中一切從全稱推出特稱(包括戾換)的推理，都是有局限性的。必須以主謂項所反映的事物存在為條件。