快速排序（Quicksort），計算機科學辭彙，適用領域Pascal，C++等語言，是對冒泡排序算法的一種改進。
基本介紹
- 中文名：快速排序算法
- 外文名：Quick Sort
- 別名：快速排序
- 提出者：C. A. R. Hoare
- 提出時間：1960年
- 適用領域：Pascal，c++等語言
- 套用學科：計算機科學
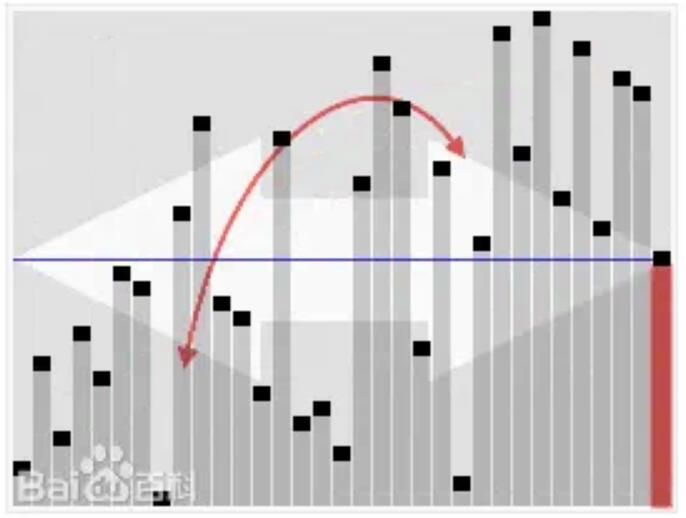
基本思想,排序流程,排序步驟,原理,排序演示,程式調用舉例,示例代碼,GO,Ruby,Erlang語言,Haskell語言,C++語言,C語言版本,Swift,Objective-C,JavaScript,Java,C#,F#,PHP,Pascal,Python3：分而治之+遞歸,Rust,性能分析,
基本思想
快速排序採用的是分治思想，即在一個無序的序列中選取一個任意的基準元素pivot，利用pivot將待排序的序列分成兩部分，前面部分元素均小於或等於基準元素，後面部分均大於或等於基準元素，然後採用遞歸的方法分別對前後兩部分重複上述操作，直到將無序序列排列成有序序列。
排序流程
快速排序算法通過多次比較和交換來實現排序，其排序流程如下：
1、首先設定一個分界值，通過該分界值將數組分成左右兩部分。
2、將大於或等於分界值的數據集中到數組右邊，小於分界值的數據集中到數組的左邊。此時，左邊部分中各元素都小於分界值，而右邊部分中各元素都大於或等於分界值。
3、然後，左邊和右邊的數據可以獨立排序。對於左側的數組數據，又可以取一個分界值，將該部分數據分成左右兩部分，同樣在左邊放置較小值，右邊放置較大值。右側的數組數據也可以做類似處理。
4、重複上述過程，可以看出，這是一個遞歸定義。通過遞歸將左側部分排好序後，再遞歸排好右側部分的順序。當左、右兩個部分各數據排序完成後，整個數組的排序也就完成了。
排序步驟
原理
設要排序的數組是A[0]……A[N-1]，首先任意選取一個數據（通常選用數組的第一個數）作為關鍵數據，然後將所有比它小的數都放到它左邊，所有比它大的數都放到它右邊，這個過程稱為一趟快速排序。值得注意的是，快速排序不是一種穩定的排序算法，也就是說，多個相同的值的相對位置也許會在算法結束時產生變動。
快速排序法對一列數字進行排序的過程圖示
一趟快速排序的算法是：
（1）設定兩個變數i、j，排序開始的時候：i=0，j=N-1；
（2）以第一個數組元素作為關鍵數據，賦值給key，即key=A[0]；
（3）從j開始向前搜尋，即由後開始向前搜尋(j--)，找到第一個小於key的值A[j]，將A[j]和A[i]的值交換；
（4）從i開始向後搜尋，即由前開始向後搜尋(i++)，找到第一個大於key的A[i]，將A[i]和A[j]的值交換；
（5）重複第3、4步，直到i==j； （3,4步中，沒找到符合條件的值，即3中A[j]不小於key,4中A[i]不大於key的時候改變j、i的值，使得j=j-1，i=i+1，直至找到為止。找到符合條件的值，進行交換的時候i， j指針位置不變。另外，i==j這一過程一定正好是i+或j-完成的時候，此時令循環結束）。
排序演示
假設一開始序列{xi}是：5，3，7，6，4，1，0，2，9，10，8。
此時，ref=5，i=1，j=11，從後往前找，第一個比5小的數是x8=2，因此序列為：2，3，7，6，4，1，0，5，9，10，8。
此時i=1，j=8，從前往後找，第一個比5大的數是x3=7，因此序列為：2，3，5，6，4，1，0，7，9，10，8。
此時，i=3，j=8，從第8位往前找，第一個比5小的數是x7=0，因此：2，3，0，6，4，1，5，7，9，10，8。
此時，i=3，j=7，從第3位往後找，第一個比5大的數是x4=6，因此：2，3，0，5，4，1，6，7，9，10，8。
此時，i=4，j=7，從第7位往前找，第一個比5小的數是x6=1，因此：2，3，0，1，4，5，6，7，9，10，8。
此時，i=4，j=6，從第4位往後找，直到第6位才有比5大的數，這時，i=j=6，ref成為一條分界線，它之前的數都比它小，之後的數都比它大，對於前後兩部分數，可以採用同樣的方法來排序。
程式調用舉例
用法:
void qsort(void *base, int nelem, int width, int (*fcmp)(const void *,const void *));
參數：
1、待排序數組首地址；
2、數組中待排序元素數量；
3、各元素的占用空間大小；
4、指向函式的指針，用於確定排序的順序。
示例代碼
GO
// 第一種寫法
func quickSort(values []int, left, right int) {
temp := values[left]
p := left
i, j := left, right
for i <= j {
for j >= p && values[j] >= temp {
j--
}
if j >= p {
values[p] = values[j]
p = j
}
for i <= p && values[i] <= temp {
i++
}
if i <= p {
values[p] = values[i]
p = i
}
}
values[p] = temp
if p-left > 1 {
quickSort(values, left, p-1)
}
if right-p > 1 {
quickSort(values, p+1, right)
}
}
func QuickSort(values []int) {
if len(values) <= 1 {
return
}
quickSort(values, 0, len(values)-1)
}
// 第二種寫法
func Quick2Sort(values []int) {
if len(values) <= 1 {
return
}
mid, i := values[0], 1
head, tail := 0, len(values)-1
for head < tail {
fmt.Println(values)
if values[i] > mid {
values[i], values[tail] = values[tail], values[i]
tail--
} else {
values[i], values[head] = values[head], values[i]
head++
i++
}
}
values[head] = mid
Quick2Sort(values[:head])
Quick2Sort(values[head+1:])
}
// 第三種寫法
func Quick3Sort(a []int,left int, right int) {
if left >= right {
return
}
explodeIndex := left
for i := left + 1; i <= right ; i++ {
if a[left] >= a[i]{
//分割位定位++
explodeIndex ++;
a[i],a[explodeIndex] = a[explodeIndex],a[i]
}
}
//起始位和分割位
a[left], a[explodeIndex] = a[explodeIndex],a[left]
Quick3Sort(a,left,explodeIndex - 1)
Quick3Sort(a,explodeIndex + 1,right)
}
Ruby
def quick_sort(a)
(x=a.pop) ? quick_sort(a.select { |i| i <= x }) + [x] + quick_sort(a.select { |i| i > x }) : []
end
Erlang語言
超簡短實現：
q_sort([])->
[];
q_sort([H|R])->
q_sort([X||X<-R,X<H])++[H]++
q_sort([X||X<-R,X>=H]).
Haskell語言
q_sort n=case n of
[]->[]
(x:xs)->q_sort [a|a<-xs,a<=x]++[x]++q_sort [a|a<-xs,a>x]
C++語言
#include <iostream>
using namespace std;
void Qsort(int arr[], int low, int high){
if (high <= low) return;
int i = low;
int j = high;
int key = arr[low];
while (true)
{
/*從左向右找比key大的值*/
while (arr[i] <= key)
{
i++;
if (i == high){
break;
}
}
/*從右向左找比key小的值*/
while (arr[j] >= key)
{
j--;
if (j == low){
break;
}
}
if (i >= j) break;
/*交換i,j對應的值*/
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/*中樞值與j對應值交換*/
arr[low] = arr[j];
arr[j] = key;
Qsort(arr, low, j - 1);
Qsort(arr, j + 1, high);
}
int main()
{
int a[] = {57, 68, 59, 52, 72, 28, 96, 33, 24};
Qsort(a, 0, sizeof(a) / sizeof(a[0]) - 1);/*這裡原文第三個參數要減1否則記憶體越界*/
for(int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
cout << a[i] << " ";
}
return 0;
}/*參考數據結構p274(清華大學出版社，嚴蔚敏)*/
C語言版本
void quickSort(int *number, int first, int last) {
int i, j, pivot;
int temp;
if (first<last) {
pivot = first;
i = first;
j = last;
while (i<j) {
while (number[i] <= number[pivot] && i<last)
i++;
while (number[j]>number[pivot])
j--;
if (i<j) {
temp = number[i];
number[i] = number[j];
number[j] = temp;
}
}
temp = number[pivot];
number[pivot] = number[j];
number[j] = temp;
quickSort(number, first, j - 1);
quickSort(number, j + 1, last);
}
}Swift
func quickSort(a: inout [Int], low: Int, high: Int) {
if low >= high { // 遞歸結束條件
return
}
var i = low
var j = high
let key = a[i]
while i < j {
// 從右邊開始比較，比key大的數位置不變
while i < j && a[j] >= key {
j -= 1
}
// 只要出現一個比key小的數，將這個數放入左邊i的位置
a[i] = a[j]
// 從左邊開始比較，比key小的數位置不變
while i < j && a[i] <= key {
i += 1
}
// 只要出現一個比key大的數，將這個數放入右邊j的位置
a[j] = a[i]
}
a[i] = key // 將key放入i的位置，則左側數都比key小，右側數都比key大
quickSort(a: &a, low: low, high: i - 1) // 左遞歸
quickSort(a: &a, low: i + 1, high: high) // 右遞歸
}
// 示例
var m = [2,3,5,7,1,4,6,15,5,2,7,9,10,15,9,17,12]
quickSort(a: &m, low: 0, high: m.count - 1)
print(m)
// 結果：[1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 9, 9, 10, 12, 15, 15, 17]Objective-C
+ (void)quickSort:(NSMutableArray *)m low:(int)low high:(int)high{
if (low >= high) {
return;
}
int i = low;
int j = high;
id key = m[i];
while (i<j) {
while (i<j && [m[j] intValue] >= [key intValue]) {
j--;
}
if (i == j) { // 當key是目前最小的數時，會出現i=j的情況，
break;
}
m[i++] = m[j]; // i++ 會減少一次m[i]和key的比較
while (i < j && [m[i] intValue] <= [key intValue]) {
i++;
}
if (i == j) { // 當key是目前最大的數時(m[j]的前面)，會出現i=j的情況
break;
}
m[j--] = m[i]; //j-- 會減少一次m[j]和key的比較
}
m[i] = key;
[self quickSort: m low: low high: i-1];
[self quickSort: m low: i+1 high: high];
// NSLog(@"快速排序 %@",m);
}JavaScript
const quickSort = (array) => {
const sort = (arr, left = 0, right = arr.length - 1) => {
if (left >= right) {//如果左邊的索引大於等於右邊的索引說明整理完畢
return
}
let i = left
let j = right
const baseVal = arr[j] // 取無序數組最後一個數為基準值
while (i < j) {//把所有比基準值小的數放在左邊大的數放在右邊
while (i < j && arr[i] <= baseVal) { //找到一個比基準值大的數交換
i++
}
arr[j] = arr[i] // 將較大的值放在右邊如果沒有比基準值大的數就是將自己賦值給自己（i 等於 j）
while (j > i && arr[j] >= baseVal) { //找到一個比基準值小的數交換
j--
}
arr[i] = arr[j] // 將較小的值放在左邊如果沒有找到比基準值小的數就是將自己賦值給自己（i 等於 j）
}
arr[j] = baseVal // 將基準值放至中央位置完成一次循環（這時候 j 等於 i ）
sort(arr, left, j-1) // 將左邊的無序數組重複上面的操作
sort(arr, j+1, right) // 將右邊的無序數組重複上面的操作
}
const newArr = array.concat() // 為了保證這個函式是純函式拷貝一次數組
sort(newArr)
return newArr
}
// 方法二：
let _quickSort = (left, right, nums) => {
let swap = (left, right, nums) => {
let temp = nums[left]
nums[left] = nums[right]
nums[right] = temp
}
if (left <= right) {
let val = nums[left]
let [i, j] = [left, right]
while (i < j) {
while (i < j && nums[j] > val) {
j--
}
while (i < j && nums[i] < val) {
i++
}
if (i < j) {
swap(i, j , nums)
}
}
nums[i] = val
_quickSort(left, i - 1, nums)
_quickSort(i + 1, right, nums)
}
}
let quickSort = (...numbers) => {
_quickSort(0, numbers.length - 1, numbers)
return numbers
}
console.log(quickSort(1, 20, 9, 13, 59, 19, 98))
Java
/**
* 入口函式（遞歸方法），算法的調用從這裡開始。
*/
public void quickSort(int[] arr, int startIndex, int endIndex) {
if (startIndex >= endIndex) {
return;
}
// 核心算法部分：分別介紹 雙邊指針（交換法），雙邊指針（挖坑法），單邊指針
int pivotIndex = doublePointerSwap(arr, startIndex, endIndex);
// int pivotIndex = doublePointerHole(arr, startIndex, endIndex);
// int pivotIndex = singlePointer(arr, startIndex, endIndex);
// 用分界值下標區分出左右區間，進行遞歸調用
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 雙邊指針（交換法）
* 思路：
* 記錄分界值 pivot，創建左右指針（記錄下標）。
* （分界值選擇方式有：首元素，隨機選取，三數取中法）
*
* 首先從右向左找出比pivot小的數據，
* 然後從左向右找出比pivot大的數據，
* 左右指針數據交換，進入下次循環。
*
* 結束循環後將當前指針數據與分界值互換，
* 返回當前指針下標（即分界值下標）
*/
private int doublePointerSwap(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int leftPoint = startIndex;
int rightPoint = endIndex;
while (leftPoint < rightPoint) {
// 從右向左找出比pivot小的數據
while (leftPoint < rightPoint
&& arr[rightPoint] > pivot) {
rightPoint--;
}
// 從左向右找出比pivot大的數據
while (leftPoint < rightPoint
&& arr[leftPoint] <= pivot) {
leftPoint++;
}
// 沒有過界則交換
if (leftPoint < rightPoint) {
int temp = arr[leftPoint];
arr[leftPoint] = arr[rightPoint];
arr[rightPoint] = temp;
}
}
// 最終將分界值與當前指針數據交換
arr[startIndex] = arr[rightPoint];
arr[rightPoint] = pivot;
// 返回分界值所在下標
return rightPoint;
}
/**
* 雙邊指針（挖坑法）
* 思路：
* 創建左右指針。
* 記錄左指針數據為分界值 pivot，
* 此時左指針視為"坑"，裡面的數據可以被覆蓋。
*
* 首先從右向左找出比pivot小的數據，
* 找到後立即放入左邊坑中，當前位置變為新的"坑"，
* 然後從左向右找出比pivot大的數據，
* 找到後立即放入右邊坑中，當前位置變為新的"坑"，
*
* 結束循環後將最開始存儲的分界值放入當前的"坑"中，
* 返回當前"坑"下標（即分界值下標）
*/
private int doublePointerHole(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int leftPoint = startIndex;
int rightPoint = endIndex;
while (leftPoint < rightPoint) {
// 從右向左找出比pivot小的數據，
while (leftPoint < rightPoint
&& arr[rightPoint] > pivot) {
rightPoint--;
}
// 找到後立即放入左邊坑中，當前位置變為新的"坑"
if (leftPoint < rightPoint) {
arr[leftPoint] = arr[rightPoint];
leftPoint++;
}
// 從左向右找出比pivot大的數據
while (leftPoint < rightPoint
&& arr[leftPoint] <= pivot) {
leftPoint++;
}
// 找到後立即放入右邊坑中，當前位置變為新的"坑"
if (leftPoint < rightPoint) {
arr[rightPoint] = arr[leftPoint];
rightPoint--;
}
}
// 將最開始存儲的分界值放入當前的"坑"中
arr[rightPoint] = pivot;
return rightPoint;
}
/**
* 單邊指針
* 思路：
* 記錄首元素為分界值 pivot, 創建標記 mark 指針。
* 循環遍歷與分界值對比。
* 比分界值小，則 mark++ 後與之互換。
* 結束循環後，將首元素分界值與當前mark互換。
* 返回 mark 下標為分界值下標。
*/
private int singlePointer(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int markPoint = startIndex;
for (int i = startIndex + 1; i <= endIndex; i++) {
// 如果比分界值小，則 mark++ 後互換。
if (arr[i] < pivot) {
markPoint++;
int temp = arr[markPoint];
arr[markPoint] = arr[i];
arr[i] = temp;
}
}
// 將首元素分界值與當前mark互換
arr[startIndex] = arr[markPoint];
arr[markPoint] = pivot;
return markPoint;
}
C#
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace test
{
class QuickSort
{
static void Main(string[] args)
{
int[] array = { 49, 38, 65, 97, 76, 13, 27 };
sort(array, 0, array.Length - 1);
Console.ReadLine();
}
/**一次排序單元，完成此方法，key左邊都比key小，key右邊都比key大。
**@param array排序數組
**@param low排序起始位置
**@param high排序結束位置
**@return單元排序後的數組 */
private static int sortUnit(int[] array, int low, int high)
{
int key = array[low];
while (low < high)
{
/*從後向前搜尋比key小的值*/
while (array[high] >= key && high > low)
--high;
/*比key小的放左邊*/
array[low] = array[high];
/*從前向後搜尋比key大的值，比key大的放右邊*/
while (array[low] <= key && high > low)
++low;
/*比key大的放右邊*/
array[high] = array[low];
}
/*左邊都比key小，右邊都比key大。//將key放在游標當前位置。//此時low等於high */
array[low] = key;
foreach (int i in array)
{
Console.Write("{0}\t", i);
}
Console.WriteLine();
return high;
}
/**快速排序
*@paramarry
*@return */
public static void sort(int[] array, int low, int high)
{
if (low >= high)
return;
/*完成一次單元排序*/
int index = sortUnit(array, low, high);
/*對左邊單元進行排序*/
sort(array, low, index - 1);
/*對右邊單元進行排序*/
sort(array, index + 1, high);
}
}
}
運行結果：27 38 13 49 76 97 65
13 27 38 49 76 97 65
13 27 38 49 65 76 97
快速排序就是遞歸調用此過程——在以49為中點分割這個數據序列，分別對前面一部分和後面一部分進行類似的快速排序，從而完成全部數據序列的快速排序，最後把此數據序列變成一個有序的序列，根據這種思想對於上述數組A的快速排序的全過程如圖6所示：
初始狀態 {49 38 65 97 76 13 27} 進行一次快速排序之後劃分為 {27 38 13} 49 {76 97 65} 分別對前後兩部分進行快速排序{27 38 13} 經第三步和第四步交換後變成 {13 27 38} 完成排序。{76 97 65} 經第三步和第四步交換後變成 {65 76 97} 完成排序。圖示
F#
let rec qsort =
function
[] -> []
|x::xs ->
qsort [for i in xs do if i < x then yield i]@
x::qsort [for i in xs do if i >= x then yield i]
PHP
<?php
$arr = array(25,133,452,364,5876,293,607,365,8745,534,18,33);
function quick_sort($arr)
{
// 判斷是否需要繼續
if (count($arr) <= 1) {
return $arr;
}
$middle = $arr[0]; // 中間值
$left = array(); // 小於中間值
$right = array();// 大於中間值
// 循環比較
for ($i=1; $i < count($arr); $i++) {
if ($middle < $arr[$i]) {
// 大於中間值
$right[] = $arr[$i];
} else {
// 小於中間值
$left[] = $arr[$i];
}
}
// 遞歸排序兩邊
$left = quick_sort($left);
$right = quick_sort($right);
// 合併排序後的數據，別忘了合併中間值
return array_merge($left, array($middle), $right);
}
var_dump($arr);
var_dump(quick_sort($arr));
Pascal
這裡是完全程式，過程部分為快排
program qsort;
var n,p:integer;
a:array[0..100000] of integer;
procedure qs(l,r:integer);//假設被排序的數組是a,且快排後按升序排列）
var i,j,m,t:integer;
begin
i:=l;
j:=r;//(l（left）,r（right）表示快排的左右區間)
m:=a[(l+r)div2];//注意：本句不能寫成：m:=(l+r)div2;
repeat
while a[i]<m do inc(i);
while a[j]>m do dec(j);//若是降序把'<'與‘>'互換;
if i<=j then
begin
t:=a[i];
a[i]:=a[j];
a[j]:=t;
inc(i);
dec(j);
end;
until i>j;
if l<j then qs(l,j);//遞歸查找左區間
if i<r then qs(i,r);//遞歸查找右區間
end;
begin
readln(n);//有n個數據要處理
for p:=1 to n do read(a[p]);//輸入數據
qs(1,n);
for p:=1 to n do write(a[p],'');//輸出快排後的數據
end.
或者
procedure quickSort(var a:array of integer;l,r:Integer);
var i,j,x:integer;
begin
if l>=r then exit;
i:=l;
j:=r;
x:=a[i];
while i<=j do
begin
while (i<j)and(a[j]>x) do dec(j);
if i<j then
begin
a[i]:=a[j];
inc(i);
end;
while (i<j)and(a[i]<x) do inc(i);
if i<j then
begin
a[j]:=a[i];
dec(j);
end;
a[i]:=x;
quicksort(a,l,i-1);
quicksort(a,i+1,r);
end;
end;
Python3：分而治之+遞歸
def quick_sort(data):
"""快速排序"""
if len(data) >= 2: # 遞歸入口及出口
mid = data[len(data)//2] # 選取基準值，也可以選取第一個或最後一個元素
left, right = [], [] # 定義基準值左右兩側的列表
data.remove(mid) # 從原始數組中移除基準值
for num in data:
if num >= mid:
right.append(num)
else:
left.append(num)
return quick_sort(left) + [mid] + quick_sort(right)
else:
return data
# 示例：
array = [2,3,5,7,1,4,6,15,5,2,7,9,10,15,9,17,12]
print(quick_sort(array))
# 輸出為[1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 9, 9, 10, 12, 15, 15, 17]
Rust
fn quick_sort<T: PartialOrd + Copy>(list: &mut Vec<T>) -> &mut Vec<T> {
if list.len() > 1 {
//獲取隨機基準值
let elme = list[rand::thread_rng().gen_range(1, list.len())];
let (mut left, mut right) = (Vec::new(), Vec::new());
//根據基準值比較,排序後的值放在左邊還是右邊
for num in list.iter_mut() {
if *num == elme {
continue;
} else if *num < elme {
left.push(*num);
} else {
right.push(*num);
}
}
//遞歸調用分治
let (mut left, mut right) = (quick_sort(&mut left), quick_sort(&mut right));
left.push(elme);
left.append(&mut right);
//由於無法返回不同的聲明周期的Vec，轉而求其次，重新賦值
list.truncate(0); //清理
list.append(&mut left); //裝彈
}
list
}
# 示例：
use rand::Rng;
fn main() {
let mut list = vec![3, 5, 8, 1, 2, 9, 4, 7, 6];
quick_sort(&mut list);
assert_eq!(list, [1, 2, 3, 4, 5, 6, 7, 8, 9]);
}性能分析
快速排序的一次劃分算法從兩頭交替搜尋，直到low和hight重合，因此其時間複雜度是O(n)；而整個快速排序算法的時間複雜度與劃分的趟數有關。
理想的情況是，每次劃分所選擇的中間數恰好將當前序列幾乎等分，經過log2n趟劃分，便可得到長度為1的子表。這樣，整個算法的時間複雜度為O(nlog2n)。
最壞的情況是，每次所選的中間數是當前序列中的最大或最小元素，這使得每次劃分所得的子表中一個為空表，另一子表的長度為原表的長度-1。這樣，長度為n的數據表的快速排序需要經過n趟劃分，使得整個排序算法的時間複雜度為O(n)。
為改善最壞情況下的時間性能，可採用其他方法選取中間數。通常採用“三者值取中”方法，即比較H->r[low].key、H->r[high].key與H->r[(low+high)/2].key，取三者中關鍵字為中值的元素為中間數。
可以證明，快速排序的平均時間複雜度也是O(nlog2n)。因此，該排序方法被認為是目前最好的一種內部排序方法。
從空間性能上看，儘管快速排序只需要一個元素的輔助空間，但快速排序需要一個棧空間來實現遞歸。最好的情況下，即快速排序的每一趟排序都將元素序列均勻地分割成長度相近的兩個子表，所需棧的最大深度為log2(n+1)；但最壞的情況下，棧的最大深度為n。這樣，快速排序的空間複雜度為O(log2n)。
