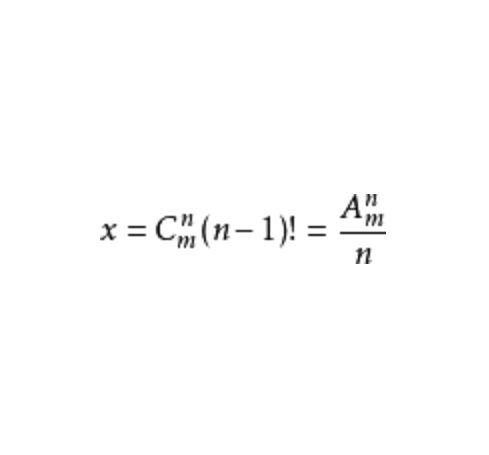循環排列

循環排列（circular permutation）亦稱圓排列、環排列等。是排列的一種，指從n個不同元素中取出m（1≤m≤n）個不同的元素排列成一個環形，既無頭也無尾。兩個循環排列相同若且唯若所取元素的個數相同並且元素取法一直，在環上的排列順序一致。

基本介紹

• 中文名：循環排列
• 外文名：Circular permutation
• 別稱：圓排列、環排列
• 定義：n個對象沿圓周的排列
• 一級學科：數學
• 二級學科：初代代數

簡介

幾個圖形按一定的規律不斷重複變化地排列，我們叫這種排列為循環排列規律，如1，2，3，

1、從1開始，然後順延，123；

2、從2開始，然後順延，231；

3、從3開始，然後順延，312。

在日常生活中和實際套用中，有時需要將元素排在封閉的曲線上。例如，慶祝節日將彩色電燈排成一個五角星形或一個圓環形；展覽會展出的商品中，有用鑽石穿成的項圈和臂鐲；開展文娛活動時，往往圍成一個圓環形進行演唱；成品加工時，有的工序安排一個圓環形，進行流水操作，像這樣元素環繞在一條封閉曲線上的排列，叫做循環排列。

圖1

如果五角星形的五個頂點，固定為V₁,V₂,V₃,V₄,V₅，或者如右圖1的圓周上編定n個不同位置的號碼為1,2,…,n，這樣，從m個相異元素里選出五個元素排在五角星形的五個頂點上，或者選出n個元素排在這圓周上，這與直線排列實無區別。但是循環排列，一般是不固定每個位置的號碼的，在這種情況下，它與直線排列就有所不同了。

例如，將a,b,c,d,e五個元素排列在圓周上，確定其中的一種，然後將各元素依順時針（或逆時針）方向繞圓周轉動一個位置，連續轉動四次（轉動五次就恢復到原來的位置），如圖2所示。連同開始的一種共得五種，在這五種排列里，元素所占的位置雖然有所改變，但元素之間的相對順序依舊未變。從a開始按順時針方向都是abcde，所以在循環排列里，這五種排列只能算作一種排列。構想在上面五個圖中的同一個方向上，如從左往右，第一個圖的e與a之間，第二個圖的d與e之間，第三個圖的c與d間，第四個圖的b與c間，第五個圖的a與b間，把各圓周剪斷，並將圓周拉成直線，則成五種不同的直線排列，它們是abcde，eabcd，deabc，cdeab，bcdea。可知五個元素的一種循環排列，對應著五種直線排列。反之，將這五種直線排列，再彎回成圓周，則又變成一種循環排列。理由很簡單，循環排列沒有首末之分，這五個元素隨便從哪一個元素開始，繞一個方向轉過去，都不改變它們的相對順序；直線排列則首末分明，原來排末位，調換排首位，已改變它們的相對順序。循環排列與直線排列的主要區別就在這一點上。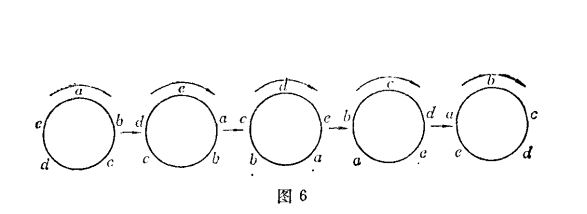

圖2

計算公式

從上文例子可以知道，五個元素的循環全排列中的一種，變成直線排列則有5種，設循環排列有x種，則直線排列有5x種，但五個元素的直線全排列有5！種，所以得到

顯然，推廣到m個相異元素，它的循環全排列的種數（設為x），仍可仿此得到，即

我們知道，從m個相異元素里，選出n個元素的直線排列的種數是，這個等式的右邊表明可以先按組合選出n個元素，然後再將選出的n個元素進行全排列，這樣，從m個元素里選出n個元素的循環排列，也可以按組合選出n個元素，然後將選出的n個元素進行循環全排列。設它的全排列種數為x，因為n個元素的循環全排列種數為（n-1）！，所以得到

在直線排列里，abcd與dcba是兩種不同的排列，這是作為平面問題來處理的。如圖3，半平面P按軸 l 翻轉180°，落在半平面Q的位置，這時abcd稱為dcba，就是說，如果不考慮元素從左到右與從右到左的方向，這兩種排列只能算一種排列。因為在生產實踐中很少遇到這種情況，所以我們沒有這樣處理直線排列問題。

圖3

在循環排列里，圖4是兩種不同的排列，這也是作為平面問題來處理的。如果作為空間問題來處理，則圓面P按軸 l 翻轉180°，落在圓面Q的位置，這時abcd成為adcb，就是說，如果不考慮元素按順時針的方向與按逆時針的方向，這兩種排列只能算一種排列。在生產實踐中要碰到這種情況。例如，圓形零件上均勻分布形式不一的小孔，就屬這種問題，遇到這種情況，使用公式計算式，需要再除以2，即四個相異元素不計順、逆時針方向的循環排列種數為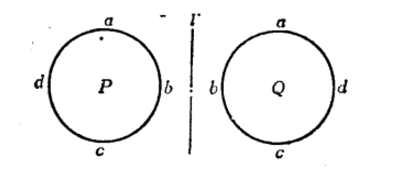

圖4

一般的，m個相異元素的循環全排列、m個相異元素里每次取出n個元素的循環排列，在不計順、逆時針方向時，它們的排列種數（設為x）分別是