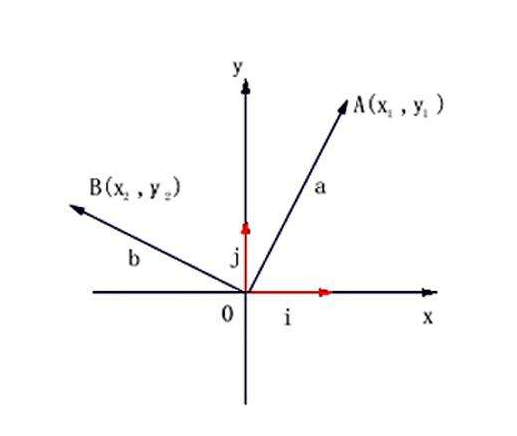
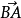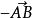在平面幾何中可以表示任意向量a的兩個非零向量e1、e2稱為平面向量基底(Plane vector basis),表示為a=xe1+ye2,用基底e1、e2表示向量a時,實數x、y的取值是唯一的。但是,能表示向量a的基底不是唯一的,也可以用基底f1、f2表示為a=mf1+nf2。
基本介紹
- 中文名:平面向量基底
- 外文名:Plane vector basis
- 適用:平面幾何問題
- 性質1:實數x、y的取值是唯一的
- 性質2:表示向量a的基底不是唯一的
- 學科:數學
平面向量基底,向量,
平面向量基底
平面上,任意向量a(包括零向量)均可用兩個非零向量(e1、e2)表示,即a=xe1+ye2(x、y為任意實數)。這就是平面向量基本定理的主要內容。這裡用來表示向量a的兩個非零向量e1、e2就稱為向量a的一組基底。注意以下幾個方面的要點:
(1)作為基底的向量不能是零向量,即e1≠0、e2≠0(這裡0指零向量);
(2)一組基底並非一個非零向量,而是指兩個非零向量;
(3)用基底e1、e2表示向量a時,實數x、y的取值是唯一的。當基底為e1、e2時,即有且只有一對實數(x,y)使得a=xe1+ye2;
(2)一組基底並非一個非零向量,而是指兩個非零向量;
(3)用基底e1、e2表示向量a時,實數x、y的取值是唯一的。當基底為e1、e2時,即有且只有一對實數(x,y)使得a=xe1+ye2;
(4)能表示向量a的基底不是唯一的。基底e1、e2可以將向量a表示為a=xe1+ye2,另外一組基底f1、f2也可以將向量a表示為a=mf1+nf2。
向量
向量,亦稱矢量。數學中最基本的概念之一。它是速度、加速度、力等這類既有大小,又有方向的量的數學抽象,常用一個拉丁字母上面加一個箭頭或用黑斜體字母表示向量,並且在向量中定義了加法和數乘這樣兩種運算。相對於向量,常把僅表示大小的量稱為數量,又稱純量或標量。近代採用向量的公理化定義,認為向量是向量空間或線性空間的元素。
在解析幾何中,常用空間的幾何線段(即有序點偶)直觀地表示向量,有時稱為幾何向量。設有向線段的始點為A,終點為B,則由它表示的向量即為 ,箭頭表示向量的方向由A到B,線段AB的長度表示向量
,箭頭表示向量的方向由A到B,線段AB的長度表示向量 的大小。A為終點B為始點的向量
的大小。A為終點B為始點的向量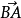 稱為向量
稱為向量 的反向量,也可記為
的反向量,也可記為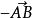 ,即有
,即有 。
。