①兩條直線被第三條直線所截,若同位角相等,則這兩條直線平行(簡稱為“同位角相等,兩直線平行”);
②兩條直線被第三條直線所截,若內錯角相等,則這兩條直線平行(簡稱為“內錯角相等,兩直線平行”);
③兩條直線被第三條直線所截,若同旁內角互補,則這兩條直線平行(簡稱為“同旁內角互補,兩直線平行”)。
基本介紹
- 中文名:平行線判定定理
- 外文名:Parallel line decision theorem
- 套用領域:數學、物理、建築學
- 類型:定理定律
定理
證明
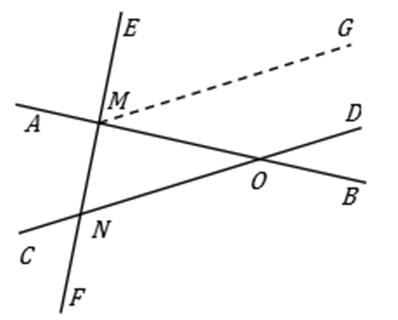
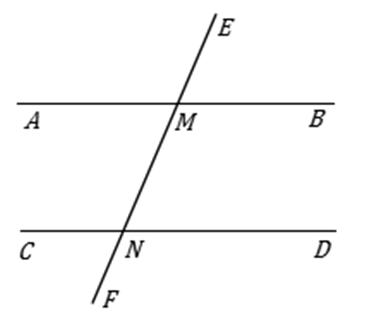
①兩條直線被第三條直線所截,若同位角相等,則這兩條直線平行(簡稱為“同位角相等,兩直線平行”);
②兩條直線被第三條直線所截,若內錯角相等,則這兩條直線平行(簡稱為“內錯角相等,兩直線平行”);
③兩條直線被第三條直線所截,若同旁內角互補,則這兩條直線平行(簡稱為“同旁內角互補,兩直線平行”)。


對平行線的判定而言,兩直線平行是結論,而對平行線的性質而言,兩直線平行卻是條件。已知兩直線平行。由平行線得到角的關係是平行線的性質,包括:①兩直線平行,同位角相等;②兩直線平行,內錯角相等;③兩直線平行,同旁內角互補。平行...
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。簡介 “幾何定理”分類 條目 平面幾何:線 平行線判定定理 平行線性質定理 垂直平分線 平行線等分線段定理...
面面平行,指的是兩個平面平行。如果兩個平面沒有公共點,則稱這兩個平面平行。如果兩個平面的垂線平行,那么這兩個平面平行。如果一個平面內有兩條相交直線與另一個平面平行,那么這兩個平面也平行。面面平行的判定定理 定理1 如果...
平行於三角形一邊,並且和其他兩邊相交的直線,所截得的三角形的三邊與原三角形的三邊對應成比例。平行線分線段成比例定理:三條平行線截兩條直線,所得對應線段成比例。推廣:過一點的一線束被平行線截得的對應線段成比例。定理推論...
第十八章 勾股定理 18.1 勾股定理 18.2 勾股定理的逆定理 第十九章 四邊形 19.1 平行四邊形 19.2 特殊的平行四邊形 19.3 梯形 19.4 重心 第二十章 數據的分析 20.1 數據的代表 20.2 數據的波動 第二十一章 二次根式 ...
74 等腰梯形性質定理 等腰梯形在同一底上的兩個角相等 75 等腰梯形的兩條對角線相等 76 等腰梯形判定定理在同一底上的兩個角相等的梯形是等腰梯形 77 對角線相等的梯形是等腰梯形 78 平行線等分線段定理如果一組平行線在一條直線上截...
定理: 兩直線平行,同旁內角互補。 【互補角相加等於180°】 逆定理 : 平行線的判定:同旁內角互補,兩直線平行。同旁內角練習 編輯 語音 1、在四邊形ABCD中,有沒有同旁內角?若有,有多少對同旁內角?
兩三角形全等。若BC=DE,反證法若BC不重合與DE,則作DE兩點與BC必有垂線段。設交點為F,G,則BF>BD-DF>0.所以不存在。所以重合。綜上,通過利用邊角邊定理,三角形三邊關係,與平行線判定定理一。我們可以得出角角邊公理 ...
24.3 平行線的判定定理 24.4 平行線的性質定理 24.5 三角形內角和定理 24.6 直角三角形全等的判定定理 24.7 線段垂直平分線的性質定理及其逆定理 24.8 角平分線的性質定理及其逆定理 一次函式 第二十四章綜合測試題 25.1 一次...
52平行四邊形性質定理1 平行四邊形的對角相等 53平行四邊形性質定理2 平行四邊形的對邊相等 54推論 夾在兩條平行線間的平行線段相等 55平行四邊形性質定理3 平行四邊形的對角線互相平分 56平行四邊形判定定理1 兩組對角分別相等的四邊...
076 角平分線的定義式 077 餘角和補角的定義式 078 對頂角的性質 079 垂線和垂線段的性質 080 平行公理 081 兩直線平行的判定定理 082 兩直線平行的性質定理 083 平行線分線段成比例定理 084 平移的性質 085 點到坐標軸的距離 086...
第五章相交線與平行線 思維導圖 知識歸納 5.1相交線 一垂線 二相交線中的角 5,2平行線及其判定 平行線 5.3平行線的性質 一平行線的性質 二命題、定理、證明 5.4平移 平移 規律方法 能力提升 第六章實數 思維導圖 知識歸納 ...
第二章 相交線、平行線 一、相交線 2.1相交線、對頂角 2.2垂線 2.3同位角、內錯角、同旁內角 二、平行線 2.4平行線 2.5平行公理 2.6平行線的判定 三、命題、定理、證明 2.7命題 2.8定理 2.9定理證明的必要性、步驟和...
