平移法作圖(construction by translation)是解作圖題的一種常用方法,利用平行移位的方法解題作圖。它分為以下兩種類型:一種是平移圖形中的幾何元素,如把一條線段移到一個新的位置並與原位置平行,使它與另一線段發生關係;一種是平移整個圖形。
基本介紹
- 中文名:平移法作圖
- 外文名:construction by translation
- 所屬學科:數學
- 所屬問題:平面幾何(尺規作圖)
- 簡介:利用平行移位的方法解題作圖
基本介紹,平移圖形中的幾何元素,平移整個圖形,舉例分析,
基本介紹
平移圖形中的幾何元素
有些幾何作圖題,需要利用平移將所求作的幾何元素或將已知幾何元素移到適當位置,使條件相對集中,構成新的容易做出的圖形。
平移整個圖形
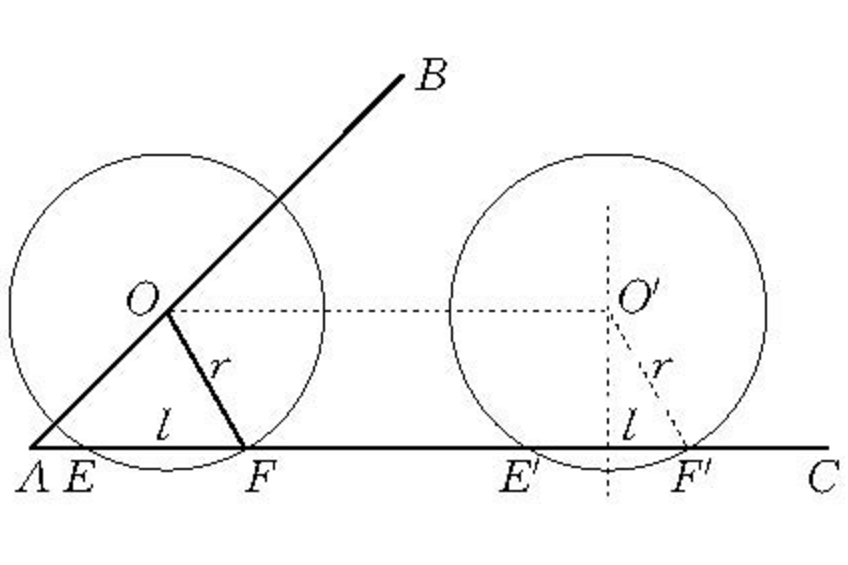
另有一些作圖題,需要暫時捨棄題中要求的某條件,首先按其他要求條件在適當位置作圖,然後利用平移將所作圖形移到能同時滿足曾暫時捨棄條件的位置。例如,已知∠BAC、線段l與r,求作一⊙O,使圓心在AB上,半徑為r,且在AC上截出的弦等於l。其思路要點是:暫捨棄圓心在AB上這一條件,半徑為r且在AC上截出的弦等於l的⊙O′容易作出(如圖1),然後將⊙O′沿CA方向平移至⊙O的位置上即為所求作的圓。當r≤l/2或E,F中一點或兩點在CA的延長線上時無解,除此以外恆有解。
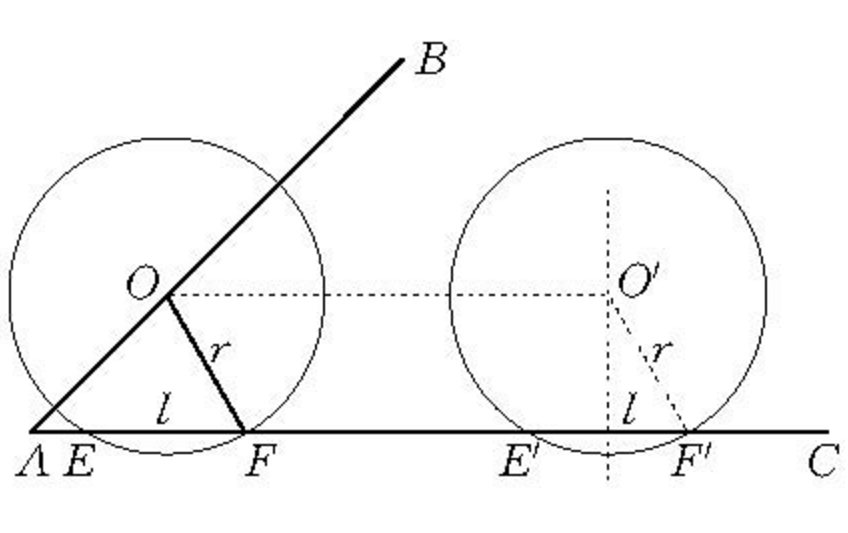
圖1
舉例分析
【例1】在兩條平行線AB和CD的兩外側有兩定點P、Q,求在AB和CD間作一條線段EF垂直於AB,交AB於E,交CD於F,使PE=QF。
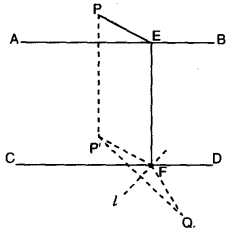
圖2
已知AB//CD,在AB和CD的兩外側有兩定點P、Q。
求作 在AB、CD間作一垂直線段EF,使PE= QF。
分析:假定EF已作出,觀察圖2,PE、QF分居在平行線的兩外側,不易發現它們的關係。若想把PE沿EF方向平移EF長度之距離,此時PE落在P'F位置上。於是P'F(代表PE)和QF集中於一處,容易發現點F位置之特點。由於P'F= PE= QF,故知點F距點P'和點Q等遠,且點F應在CD上,所以只要點P'位置定了,點F位置也可隨之確定。
作法:
(1)設AB和CD的距離為d,由P點作AB之垂線PP'且截取PP'= d;
(2)連結P'Q。
(3)作P'Q之垂直平分線l交CD於點F。
(4)由點F作FE⊥CD,交AB於E,則EF就是所求作的線段。
證明:依作法, ,且P'P//EF,所以PP'FE為平行四邊形,有PE= P'F,又因l是P'Q的垂直平分線,所以P'F= QF,所以PE= QF。
,且P'P//EF,所以PP'FE為平行四邊形,有PE= P'F,又因l是P'Q的垂直平分線,所以P'F= QF,所以PE= QF。

討論:由題設可知,PQ必與CD相交。設點P與AB的距離為d1,點Q與CD的距離為d2。
(1)PQ與CD直交,這時P'Q也與CD直交;
1' 當d1=d2時,線段P'Q的垂直平分線l與CD重合。這時,AB和CD的任意一條公垂線EF都符合條件,因此在這種情形下本題有無窮多個解。
2' 當d1≠d2時,線段P'Q的垂直平分線l不與CD重合,而與CD平行,即l與CD沒有交點,這時本題無解。
(2)PQ與CD斜交,這時P'Q也與CD斜交,因此,線段P'Q的垂直平分線l與CD有一個交點F,這時本題有一解。
使用平移法作圖,關鍵在於通過平移,能夠使條件集中或分散。一般地說,與平行線有關的問題,定向定長線段的定位問題,兩圓公切線問題,四邊形問題等,都可優先考慮用平移法。
使用平移法作圖,在作圖分析中應弄清楚平移方向是什麼,平移距離是多少,把什麼圖形平移,等等。