希爾霍爾策算法

一種用來尋找歐拉迴路的圖算法。由數學家卡爾·希爾霍爾策給出。使用了類似貪婪法的思路。右圖給出了一個用該算法尋找歐拉迴路的例子。

基本介紹

• 中文名：希爾霍爾策算法
• 外文名：Hierholzer's algorithm
• 所屬學科：數學、圖論、計算機科學
• 釋義：一種尋找歐拉圖中歐拉迴路的算法

定義

希爾霍爾策算法是數學家卡爾·希爾霍爾策在1873年提出的一種尋找歐拉迴路的算法。比起另一種著名的Fleury算法而言，希爾霍爾策算法更加高效，能夠達到圖的總邊數的線性次複雜度。

算法過程

下面給出來自Harris的《Combinatorics and Graph Theory》中對該算法的描述：現給出一個歐拉圖G，求歐拉迴路。

1. 選定G中一個環，稱其為R1，標記R1的邊，並記i為1。
2. 如果Ri已經包含G中所有邊，則停止搜尋，顯然Ri已經是一個歐拉環路。
3. 否則，取Ri中一個點vi，滿足vi有一條未被標記的邊，記作ei。
4. 從vi和ei出發，尋找一個環Qi，標記Qi上的所有邊
5. 使用Qi，創建一條新的環Ri+1
6. i的值加一，並回到步驟二，如此重複。

希爾霍爾策算法的示例可見圖例“希爾霍爾策算法示例”。其中每個圖中被標粗的是被選中的邊，R表示當前已得到的總環路，Q表示當前一輪得到的環路。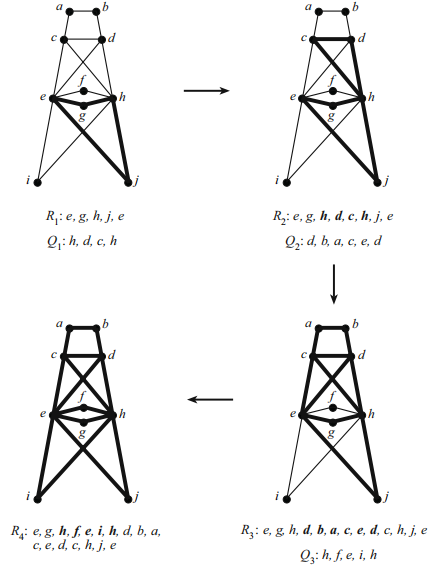

希爾霍爾策算法示例

正確性說明

實際上每次從歐拉圖中取走一個環路不會影響歐拉圖每個度為偶數的性質，因為環上各個點的度同樣為偶數。因此在算法運行過程中，每一輪過後沒有標記的邊依然會組成歐拉圖。而每一次過程中必然會取出一定數量的邊（否則就會停止，表明已經獲得了歐拉迴路），圖的邊數一定，因此一定會有一輪能夠取完所有的邊。因此該算法最終可以得出歐拉迴路。