布隆斯公式

定義

物理大地測量學中的基本公式。即由擾動位計算大地水準面起伏的公式，即

式中γ為平均橢球體表面的正常重力，可用全球平均值

代替；T₀為大地水準面上的擾動位。

如圖1所示，設p₀在大地水準面上，它在地球橢球體面上的投影為p₀'，兩點之間的距離為N，它稱為大地水準面相對於地球橢球體面的高，是一個不大於150米的變數。

大地水準面上p₀點的重力位為：

式中，U(p₀)是p₀點的正常重力位，T(p₀)是相應的擾動位。

而地區橢球體面上p₀點的正常重力位為：

又

由以上三式得：

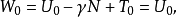
所以

這就是著名的布魯斯公式。它建立了擾動位和大地水準面起伏之間的關係，是重力學的基本公式之一。

以布魯斯公式為出發公式，式中γ是已知量，所以只要給出由重力異常⊿g求T的具體形式，問題也就解決了。T可以有級數形式，也可以有積分形式。因此求大地水準面高度的公式也有級數形式和積分形式。

式中，r為大地水準面到地心的距離，

接近於1，所以上式變成

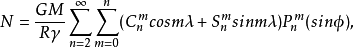
作為球近似，

，於是上式近似形式為

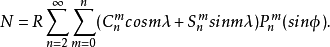
以上三式便是求大地水準面高度的級數公式。由於目前所求得的球諧函式係數，無論是階次還是精度都滿足不了本問題的要求，所以有必要推導積分公式。

根據本問題的精度要求，得到

這就是求大地水準面高度的斯托克司積分公式。只要我們已知整個大地水準面的(g₀-γ₀)，就可以用數值積分法求出大地水準面的高度N。