布拉施克度量(Blaschke metric)仿射空間中超曲面上的仿射不變的黎曼度量.設M是n}-1維仿射空間中的超曲面，二是位置向量，}u' }u2, ".. }u"}}是局部坐標.
若
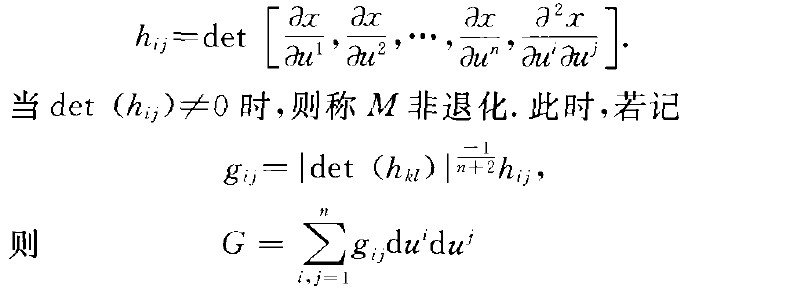
在M上定義了一個仿射不變的偽黎曼度量，稱為布拉施克度量.當M局部嚴格凸時，可選擇M的定向，使布拉施克度量正定.
布拉施克度量
相關詞條
- 布拉施克度量
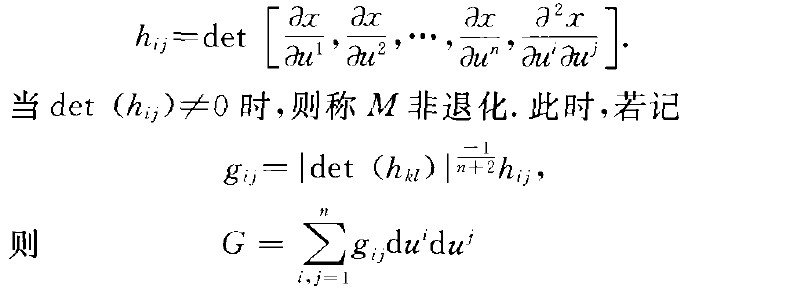
布拉施克度量(Blaschke metric)仿射空間中超曲面上的仿射不變的黎曼度量.設M是n}-1維仿射空間中的超曲面,二是位置向量,}u' }u2, ".. }u"}}是局部坐標...
- 布拉施克
布拉施克(Blaschke ,Wilhelm Johann Eugen),德國數學家。代表作《微分幾何講義》。... 布拉施克於1921年在文獻中猜想,任何再見曲面必為具有常曲率的 黎曼度量的2-...
- 仿射法線
若M是n+1維仿射空間An+1中的非退化超曲面,x是位置向量,Δ是關於布拉施克度量的拉普拉斯運算元,則Y=Δx/n是M上仿射不變的橫截向量場,稱為M的仿射法向量場。
- 仿射球面
因此,對仿射球面的分類是基本的、重要的.關於布拉施克度量完備的局部嚴格凸仿射球面的整體分類始於布拉施克(Blaschke,W.J.E.),他於1923年證明:一個緊緻無邊的2...
- 仿射極大曲面
於1986年提出了下面的問題:關於布拉施克度量完備的仿射極大曲面一定是橢圓拋物面嗎?陳省身的猜測和卡拉比的問題都稱為仿射伯恩施坦問題.這個問題最近被塔丁格(...
- 富比尼一皮克形式
purr)是局部坐標.M上可以定義兩個聯絡:一個為A..+}的聯絡通過仿射法線在M上的誘導聯絡,用rkrJ表其聯絡係數;另一個是M上布拉施克度量的列維-齊維塔聯絡,用幾...
- 仿射微分幾何基本定理
仿射微分幾何基本定理(fundamental theoremof affine differential geometry)關於仿射空間中的超曲面完全由布拉施克度量和富比尼一皮克形式確定的定理.設在一個n維單連通...
