定理機器證明是用計算機自動地進行推理和證明數學定理。又稱為自動定理證明(ATP)。讓機器去證明數學定理的想法,在17世紀G.W.Leibniz 創立數理邏輯時就產生了,但這一想法的真正實現,是在20世紀40年代計算機誕生以後。
基本介紹
- 中文名:定理機器證明
- 外文名:mechanical theorem proving
- 機器:計算機
- 套用:各種人工智慧系統
- 作用:推理和證明定理
簡介
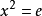

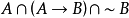
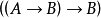
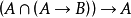

定理機器證明是用計算機自動地進行推理和證明數學定理。又稱為自動定理證明(ATP)。讓機器去證明數學定理的想法,在17世紀G.W.Leibniz 創立數理邏輯時就產生了,但這一想法的真正實現,是在20世紀40年代計算機誕生以後。
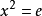

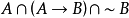
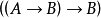
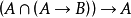
定理機器證明是用計算機自動地進行推理和證明數學定理。又稱為自動定理證明(ATP)。讓機器去證明數學定理的想法,在17世紀G.W.Leibniz 創立數理邏輯時就產生了,但這...
把人證明數學定理和日常生活中的演繹推理變成一系列能在計算機上自動實現的符號演算的過程和技術,又稱自動定理證明和自動演繹。...
機器證明及其套用是中國攀登計畫項目之一。該項目的核心內容主要是幾何定理機器證明和非線性代數方程組理論、算法和套用。...
《非線性代數方程組與定理機器證明》是1996年上海科技教育出版社出版的圖書,作者是楊路,張景中,侯曉榮。...
圖集 平面幾何定理的機器證明圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近更新: 創建者:微笑●L62猜你關注...
《論初等幾何定理的機器證明與消去法》是2016年3月出版的圖書,作者是朱望規。...... 《論初等幾何定理的機器證明與消去法》是2016年3月出版的圖書,作者是朱望規...
方法優點之一是占用記憶體小,至今是唯一可用袖珍計算機證明非平凡幾何定理的方法,也是機器證明中唯一可高度並行的算法。在國外文獻中稱此法為“楊張定理”。用此法...
另一方面,將系統劃分為小的組件可降低各部分的複雜性,並可以使用定理機器證明(automated theorem proving)來證明關鍵的軟體子系統的正確性。因此,當單一的有特點的...
1992年張景中等提出了幾何定理可讀證明自動生成的理論、算法和方法,並實現為通用的微機程式。用此新方法已經證明近千個非平凡的幾何定理,其中有幾十個非歐幾何的新...
張院士主要從事機器證明、教育數學、距離幾何及動力系統等 張景中 領域的研究。其主要貢獻是:(一)提出了面積解題方法,並用之於機器證明的研究,使幾何定理可讀證明的...
數學機械化研究,是在初等幾何定理的機器證明研究方面取得突破的。公理化體系的幾何定理證明非常不機械化。以中學課程中的幾何為例,-個定理的證明,往往要經過冥思苦...
九州電器、東方電機等三十餘家單位進行了科研項目合作,還面向海內外舉辦多場自動推理(定理機器證明)研究進展的講座,極大地提升了實驗室的實力,為此次申報成功奠定了...
王湘浩在定理機器證明的歸結方法上做出了研究成果。1982年王湘浩和他的學生研究了歸結方法中的取因子問題並提出了廣義歸結方法。廣義歸結方法包含了普通歸結方法(J...
另一方面,將系統劃分為小的組件可降低各部分的複雜性,並可以使用定理機器證明(automated theorem proving)來證明關鍵的軟體子系統的正確性。因此,當單一的有特點的...
隨後,邏輯程式設計得到了迅速發展,特別是基於一階謂詞的邏輯程式設計語言,將邏輯推理對應於計算,具有豐富的表達能力、非確定性等特點,在定理機器證明、關係資料庫系統...
(4) 定理機器證明與自動推理平台(973,2003-2004年,子課題承擔人)(5) 偏序時序邏輯及其模型檢測(德國DFG,2004-2005年,聯合主持)...
幾何定理的機器證明 數學的機械化問題 數學中的公理化與機械化思想 幾何定理機器證明 初等幾何判定問題與機械化證明 幾何學機械化方法及其套用 數學的機械化與機械化...
劉敘華,教授,博士生導師。1937年生,黑龍江哈爾濱人。1961年吉林大學數學系畢業,留校任教。1985~1986年在美國依利諾大學計算機系作訪問學者。主要從事定理機器證明和...
