完全碼

完全碼(perfect code)是一類特殊的碼。

設C是碼長n的q元線性碼，並假定C是可以糾正t個差錯的碼，那么所有重量≤t的差錯模式都分屬於C的不同的陪集．如果所有重量≤t的差錯模式所屬的C的陪集的並正好是Vn(Fq)，那么C就叫完全碼．換句話說，如果C的每個陪集中都含有一個而且唯一的一個重量≤t的差錯模式，C就叫完全碼．

基本介紹

• 中文名：完全碼
• 外文名：completecode/perfect code
• 所屬領域：數理科學
• 相關概念：Hamming碼

定義

定義一

設Q是一個含q個字母(或元素)的字母集，q是任意一個正整數．令那么I l=q．我們把 叫做字的集合，而把 的子集叫做碼長n的q元碼．可以在 中引進Hamming距離．設a=(a1，a2，…，an)，b=(b1，b2，…，bn)∈ ．令

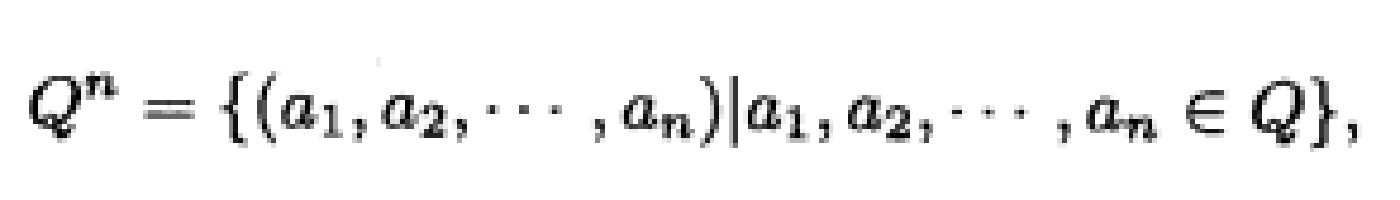
我們把ρ(a，b)叫做a和b的Hamming距離．設C是一個碼長等於n的q元碼，並假定C是可以糾正t個差錯的糾錯碼．設c∈C，令

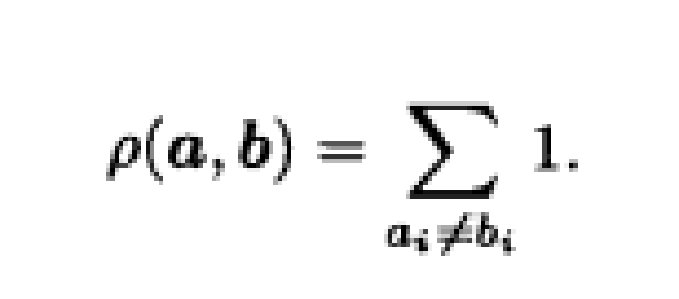
即 (c)是由與c的距離≤t的所有的字所組成的集合．我們把 (c)叫做以c為中心，以t為半徑的球．因C可以糾正t個差錯，所以當c1，c2∈C而c1≠c2時， (c1)和 (c2)就沒有公共元素．如果

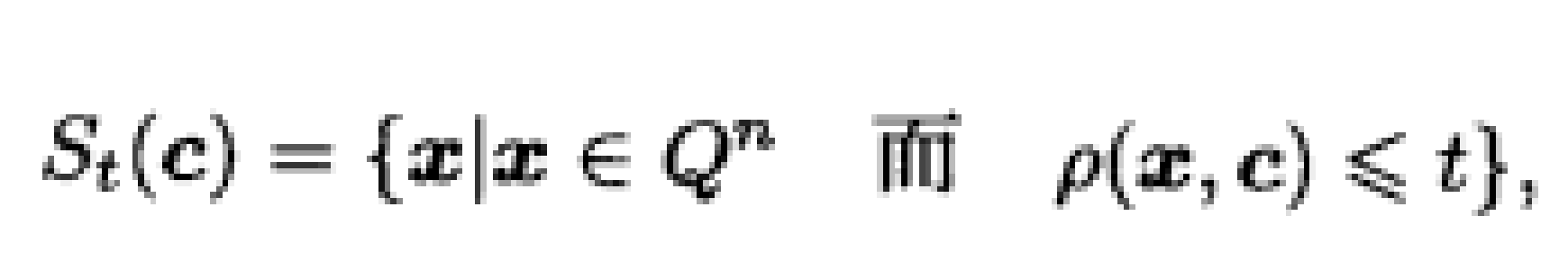
即 分成兩兩沒有公共元素的球 (c)，c∈C的並，我們就說C是完全碼．換句話說，如果任意一個字都屬於一個而且唯一的一個球 (c)，c∈C，我們就說C是完全碼．

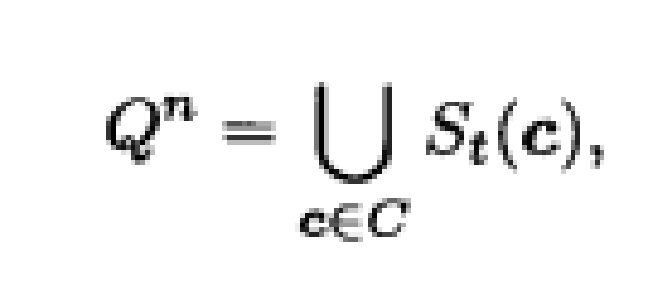
定義二（見概述）

相關定理

定理1 二元( 一1， 一1一r)Hamming碼是完全碼．

定理2 對於線性碼來說，定義1和定義2是等價的．

意義

完全碼的意義在於，收方無論收到哪一個字都可以確定把它譯成哪個碼字，而不會發生解碼不能確定的情形．譬如，設C是可以糾正t個差錯的q元完全碼，q是任一正整數．當收方收到x這個字時，因x一定屬於一個而且唯一的一個球 (c)，c∈C，那么x和c的距離≤t而x和其餘碼字的距離一定大於t．因此根據極大似然解碼方法，就應把x譯成c．從解碼表來說，完全碼的解碼表中沒有虛線，或者說虛線下面沒有字．但這並不排斥可能發生解碼錯誤的情況．特別，如果一個碼字在傳送過程中有≥t+1個碼元被傳錯，那就肯定發生解碼錯誤．