多維信號處理

多維信號處理（Multidimensional signal processing）作為信息的不同表達形式，在分析和處理上與一維具有很多相似之處，許多一維的處理方法可直接推廣到多維。但多維信號的自由度的增加導致了在一維不曾遇到的設計及處理上的靈活性，這一方面提高了多維信號處理的複雜程度，另一方面也為問題的解決提供了更多的途徑。

基本介紹

• 中文名：多維信號處理
• 外文名：Multidimensional signal processing
• 縮寫：MSP
• 涉及領域：信息科學
• 目的：信息表達
• 優點：自由度的增加

背景

近代計算技術的高度發展，誕生了數字信號處理這個全新的研究領域。由於需要大量的數字存儲及計算量，多維信號處理在近幾年才發展起來。作為信息的不同表達形式，多維信號在分析和處理上與一維具有很多相似之處，許多一維的處理方法可直接推廣到多維。但多維信號的自由度的增加導致了在一維不曾遇到的設計及處理上的靈活性，這一方面提高了多維信號處理的複雜程度，另一方面也為問題的解決提供了更多的途徑。

由於取樣在多維空間中進行，多維信號的離散化不僅可以調整取樣速率，且可調整取樣的幾何方式。不同的取樣方式決定了相應的信號處理方法的效率。矩形取樣的優點在於其分析和實現上的簡便性，而六角取樣在某些情況下具有最佳的取樣效率，在信號處理中如能靈活運用各自的特性，將二者有機地聯繫起來，這對於多維信號處理系統的簡化具有重要意義。

簡介

為了在時間、頻率、幅度、到達方向和極化等域中對信號能量進行檢測和定位，需要多維處理(MDP)。這種方法的主要優點來源於以下幾種可能性，即收集更多的能量的可能性，利用不同信號域之間的交叉信息的可能性以及降低在所有信號域中同時出現干擾的機率的可能性。它給採用MDP原理設計的雷達一些有益的影響，例如改善檢測、在決定目標的位置、延伸性和形狀方面有更好的準確度和解析度，以及減少加在有用信號上的干擾的影響等。

多維處理意味著產生多功能信號波形並且以適當的方式順序的發射和接收。這種信號是編碼的，其綜合結果能給雷達提供一個包括時間域、頻率域、幅度域甚至極化域的工作環境，發射與接收天線系統應保障這種波形編碼，並有助於在角度域中工作。此外，處理器應處理屬於多個域的數據(矢量處理方式)。目前還沒有一種適於處理這種多個域的編碼波形的設計及其相應的矢量代處理結構的統一的理論。

信號處理

信號處理(signal processing) 是對各種類型的電信號，按各種預期的目的及要求進行加工過程的統稱。對模擬信號的處理稱為模擬信號處理，對數位訊號的處理稱為數位訊號處理。所謂"信號處理"，就是要把記錄在某種媒體上的信號進行處理，以便抽取出有用信息的過程，它是對信號進行提取、變換、分析、綜合等處理過程的統稱。

數位訊號處理是20世紀60年代才開始發展起來的，開始是貝爾實驗室及麻省理工學院用電子計算機對電路與濾波器設計進行仿真，奠定了數字濾波器的發展基礎。60年代中期，發明了快速傅立葉變換，使頻譜分析的傅立葉分析的計算速度提高了百倍以上，從而達到了可以利用電子計算機進行譜分析的目的，奠定了信號與系統分析的實用基礎，形成了以數字濾波及快速傅立葉變換為中心內容的數位訊號處理的基本方法與概念。70年代開始，數位訊號處理這個專用名詞在科技領域問世。

模擬信號的離散化

矩形取樣與六角取樣的效率

二維模擬信號的離散化是在平面上進行的，取樣點的位置取決於二個方向，因此具有多種不同的取樣方式。在二維情況下，矩形和六角取樣均可在頻域構成允許覆蓋。若區域R具有允許覆蓋，則其時域的取樣密度與R的面積成正比。因此要想得到小的取樣密度，應適當選取基帶R，使信號在不產生混迭的條件下R的面積達到最小。

區域R具有兩重意義，當它表示模擬信號二。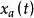的頻譜支撐時，若其具有允許覆蓋，由於面積的確定，其周期延拓方式對取樣率不產生影響，因此不同取樣方式對應同樣的取樣密度。若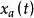的頻譜支撐不具有允許覆蓋，則必須對其進行擴充，此時R表示擴充後的頻譜基帶。R的擴充方式決定了時域的取樣方式，擴充部分不包含任何信息，在這種情況下信號的取樣率隨R的面積的減小而減小。例如對於具有循環對稱頻譜的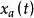，由於圓形區域不具有允許覆蓋，因此須對其進行擴充。六角擴充的面積較之矩形節省13.4000取樣點的減少意味著所需運算量和存儲量的減少，這對多維信號處理是很有意義的。

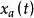
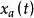
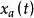
六角取樣序列及其頻譜

六角取樣序列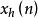及其頻譜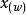

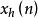
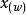
無論用何種取樣方式得到離散信號，由於它們是對同一信號的不同描述，均包含恢復原信號所需的足夠信息，因此其分析和處理可拋開原來的摸擬模型獨立地進行。通常將信號視作取樣的集合而不是函式，這對問題的解決是很有幫助的。

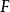對於序列定義變換:

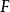
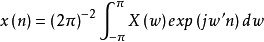
式中為任意離散序列，與取樣方式無關。

由同一連續信號採取不同的取樣方式所得的序列，由於取樣點的位置不同，表示為完全不同的序列，因此根據(1)式得到的數字頻譜完全不同。但因為基於同一信號，各種表達方式之間有著內在的聯繫，在頻譜上表現為數字頻率ω與模擬頻率τ的轉換關係上。對於矩形取樣:

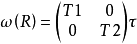
即表現為座標刻度的改變；對於六角取樣：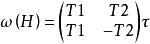

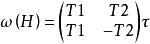
不僅刻度改變，而且座標軸本身產生旋轉。因為有效頻譜相同，所以有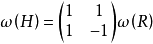

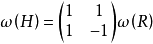
六角取樣與矩形取樣在時頻域的關係如圖1所示:

因此，作為矩形取樣信號處理的六角取樣信號只要對其作變換

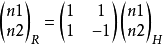
即可恢復各取樣點在模擬域的幾何位置，頻譜做變換

可得到對應的矩形取樣序列的數字譜。這樣六角取樣序列的處理分解為矩形處理加一線性變換(或稱座標旋轉)，座標旋轉的目的是恢復取樣點在模似平面上的幾何位置。因為在離散序列的處理過程中信號僅作為取樣的集合，與其在時域中點的位置無關，因此線性變換隻是觀念上的，並不作實際轉換處理，所以並不增加運算量。

由此我們得出結論：在DSP中無需考慮信號的來源。在模擬向數位訊號轉換過程中選取最佳的取樣方式以得到最佳的取樣效率。離散序列一經得到，即可將其視為一組數的集合，用簡便的矩形處理技術處理信號的恢復工作，即數一模轉換，藉助座標旋轉便可實現。