埃爾布朗一哥德爾部分可計算函式是美國邏輯學家、數學家克林(Kleene , S. C.)於1936年定義一類函式的數學術語。
基本介紹
- 中文名:埃爾布朗一哥德爾部分可計算函式
- 提出者:克林(Kleene , S. C.)
- 提出時間:1936年
- 適用領域:數學、函式
遞歸函式伽-recursive function是由美國邏輯學家、數學家克林(Kleene , S. C.)於1936年首先定義的一類函式.它是由本原函式出發,經過疊置,原始遞歸及屍遞歸(即屍運算元)作用而得的函式.嚴格地講,屍遞歸函式類是滿足下列條件的最小(全)函式類C:
1.本原函式在C中.
2.C關於疊置封閉.
3.C關於原始遞歸式封閉.
4.C關於產運算元封閉.
產遞歸函式恰好為HU可計算函式,它們都是直觀上能行可計算的函式,在上述定義中,若允許部分函式,便得到部分遞歸函式.此外,只要在上述定義中
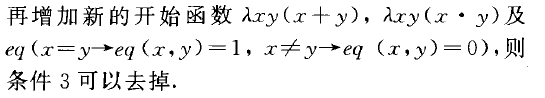
公式
由克林足義的產遞歸函式.簡稱遞歸函式.遞歸函式有許多種等價定義形式:埃爾布朗一哥德爾一般遞歸函式(即HU可計算函式)、由一般遞歸式定義的一般遞歸函式、圖靈可計算全函式等.遞歸函式類是原始遞歸函式類乃多重遞歸函式類的真擴張,又是部分遞歸類的真子類.但是與其他幾個函式類不同,遞歸函式類是不可能行地列舉出來的.
