基本介紹
- 中文名:地轉流
- 外文名:geostrophic current;geostrophic flow
- 類型:海洋流
- 影響因素:海水密度
相關定義,計算測量,特點,地轉方程,相關因素,動力計算,
在水平壓強梯度力的作用下,海水將在受力的方向上產生運動。與此同時科氏力便相應起作用,不斷地改變海水流動的方向,直至水平壓強梯度力與科氏力大小相等方向相反取得平衡時,海水的流動便達到穩定狀態。若不考慮海水的湍應力和其它能夠影響海水流動的因素,則這種水平壓強梯度力與科氏力取得平衡時的定常流動,稱為地轉流。
相關定義
定義1:海洋學中與海水水平壓強梯度相聯繫的一種海流。 所屬學科: 大氣科學(一級學科) ;套用氣象學(二級學科)
定義2:水平壓強梯度力和科氏力平衡條件下的海流。
所屬學科: 海洋科技(一級學科) ;海洋科學(二級學科) ;物理海洋學(三級學科)。
計算測量
在忽略湍流摩擦力作用的較深的理想海洋中,由海水密度分布不均勻所產生的水平壓強梯度力與水平地轉偏向力平衡時的海流。雖然它和埃克曼漂流都是理想化的海流,但都能近似地反映海水的一些運動規律。例如:較厚的大洋下層水中的海流,近似於地轉流;在較薄的大洋上層水中,同時存在著地轉流和埃克曼漂流。這兩種流動同為大洋的基本流動。
要直接測量海洋的水平壓強梯度力是很難的,但是可以引進地勢的概念,間接加以計算。構想在較深海洋中的某水層,其等壓面和地勢面重合,則在這個面上的地轉流的速度為零。稱這個面為無運動面。等壓面上相鄰兩點間的地勢差,稱為動力高度差。
實際上,要測定大範圍海域中各點的流速是困難的,但要測定此海域中各點的海水比容是辦得到的,而且由這些比容按動力計算法求得的地轉流,又與較深海洋的下層海水的流動近似,故可以用這種海流的動力計算,代替較深層海流的測定。
特點
1)地轉流流速大小與等壓面和等勢面的夾角的正切成正比,與科氏參量成反比;
2)沿兩面的交線流動, 北半球流向偏在壓強梯度力水平分力右方90度;
3)在北半球,面向流去的方向,右面等壓面高,左面低。
4)內壓場引起的等壓面傾斜主要體現在海洋的上層,隨深度增加而減小。外壓場引起的等壓面傾斜則直達海底。
地轉方程
為討論簡便起見,設等壓面只沿直角坐標系的x軸方向傾斜,它與等勢面的夾角為β,如圖5-4所示。此時海水運動方程簡化為(圖1)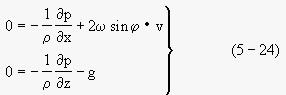 圖1
圖1
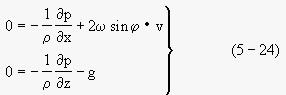 圖1
圖1第二式即為靜力方程。由第一式直接可得(圖2)
上述情況下,地轉流向沿y軸方向,且在等壓面與等勢面的交線上流動。在北半球垂直於壓強梯度力指向右方,當觀測者順流而立時,右側等壓面高,左側低。即等壓面自左下方向右上方傾斜。在南半球則與之相反。
在整個海洋中由內壓場與外壓場導致的地轉流卻具有其特定的分布形式。由內壓場導致之地轉流,一般隨深度的增加流速逐步減小,直到等壓面與等勢面平行的深度上流速為零;其流向也不盡相同,有時稱其為密度流。由外壓場導致的地轉流,自表層至海底(除海底摩擦層外),流速流向相同,有時稱其為傾斜流。然而在實際海洋中,地轉流往往是在總壓場作用下引起的。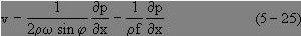 圖2
圖2
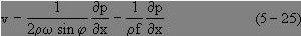 圖2
圖2相關因素
海洋中的密度變化是連續的,因此,由於海水密度分布不均勻產生斜壓場引起的地轉流場的變化也應當是連續的。但為了簡便起見,僅取兩層密度不同的海水加以討論。設上下層海水密度分別為ρ1與ρ2,且ρ2>ρ1。在海水靜止時,其界面應是水平的。然而當上下層海水分別以流速v1與v2流動時,則界面一般不會再是水平的,而會發生傾斜,設其相對x軸的傾角為γ。另外設等壓面也只在x軸方向傾斜,上下兩層海水等壓面的傾角分別為β1與β2。海水只在y軸方向流動。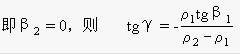 圖5
圖5
 圖5
圖5通過兩層海水界面時海水的壓力變化是連續的,界面上任意兩點之間的壓力差為dp,即有dp1=dp2
(圖3)此式可套用於密度連續變化的海洋中。 圖3
圖3
 圖3
圖3(圖4)式(5—28)和(5—29)兩式給出了密度界面(在密度連續變化的海洋中為等密度面)的傾角與流場、壓力場之間的相互關係。可見只有在ρ2v2=ρ1v1,即上下兩層海水的動量相等時,界面才是水平的,這在海洋中,特別是大洋上層一般難以滿足,因為等密度面通常是傾斜的。
不過在赤道例外,因為那裡f=0,所以tgγ=0。 等密度面的傾角比等壓面的傾角大得多,一般為等壓面傾角的102~103倍。這就為利用密度場描述地轉流提供了方便條件。實際海洋中的地轉流流速,一般是上層大於下層,不難從式(5—29)中看出,設v2=0,(圖5)
因為ρ2>ρ1,故上式永遠為負值,即tgβ1與tgγ符號相反,說明等壓面與等密面相對x軸傾斜方向相反。反之,當上層流速小於下層流速時,則等壓面與等密面的傾斜方向相同。但這在海洋中比較少見。 圖4
圖4
 圖4
圖4上述關係可用下述法則綜合:當上層流速大於下層流速時,順流而立,則在北半球密度小的海水在右側,密度大的海水在左側,等壓面自左向右上傾斜。在南半球則相反。海水密度,特別在大洋上層,其水平分布主要由溫鹽決定,因此等密面的傾斜方向通常與等溫面和等鹽面的傾斜方向相同,從而與等壓面的傾斜方向相反。實際工作中常常可以根據等溫面(線)或等鹽面(線)的傾斜方向定性地推知地轉流的方向。
動力計算
由地轉流公式可知,只要知道等壓面相對等勢面的傾角,就可計算地轉流速。但是等壓面的傾角量級大小,至今難以直接測量。因此只有藉助于海洋調查中的溫度、鹽度和深度(壓力)資料,根據海水狀態方程,首先計算海水的密度或比容,進而計算等壓面之間的位勢差,再進行地轉流的計算。
計算公式
計算公式(海蘭—漢森公式) 圖6
圖6
 圖6
圖6設在垂直於地轉流向的鉛直斷面上取相距L的兩個測站A0與B0,如圖5-6所示。Φ0、Φ1、Φ2與p0,p1,p2分別為等勢面與等壓面,β0、β1、β2為等壓面的傾角,v0、v1、v2分別為等壓面p0、p1、p2上的流速,則(圖6)
其中B1B2與A1A2分別為p1與p2等壓面之間在B0與A0站的鉛直幾何距離,根據關係式(圖7)
它們可以用位勢差表示,則有(圖8)
ΔΦB、ΔΦA分別為pl與p2等壓面之間在B0與A0站的位勢差。其計算方法由式(5—11)給出。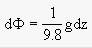 圖7
圖7
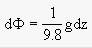 圖7
圖7必須指出,由式(5-30)計算的流速是p1等壓面相對p2等壓面的流速,並非相對靜止海底的絕對流速。同理可計算自海面至海底任何兩等壓面之間相對流速。
流速參考零面的選取
為求得各層相對海底的絕對流速,必須在海洋中選取一個流速為零的參考面。在大洋中這個面是可以找到的,具體方法讀者可參考有關專門文獻,不作進一步介紹。至於淺海中零面的選取,可近似地視海底為零面,然後對不同深度的海底進行訂正即可。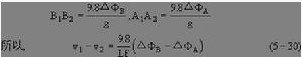 圖8
圖8
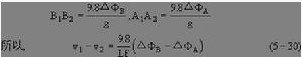 圖8
圖8由於動力計算方法是計算不同傾斜角度的兩等壓面之間的相對流速,所以它只適應於內壓場引起的地轉流的計算,對外壓場導致的傾斜流,不能用此法進行計算。因為外壓場中自表至底各等壓面都是平行的,其傾角相同,因此各等壓面之間的相對流速都為零。
實際工作中,由於事先無法了解地轉流向,在布設調查斷面時難以與其垂直。因此,通常在調查海區中布設多個測站,然後根據調查資料計算每個測站相應等壓面的位勢差,據此繪製位勢高度等值線(圖5—7)。高值中心,表示等壓面上凸,低值中心表示等壓面下凹。根據壓力場與流場的關係,不難理解這些等位勢高度線就是地轉流向線。在北半球,繞高值中心的流動方向為順時針,繞低值中心的流動方向為反時針。在南半球相反。而且等位勢高度線密集處流速大,稀疏處流速小。