四元式

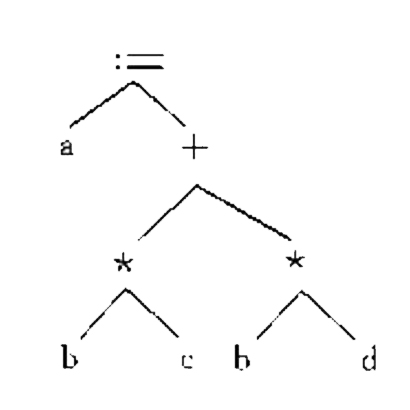
四元式是一種更接近目標代碼的中間代碼形式。由於這種形式的中間代碼便於最佳化處理，因此，在目前許多編譯程式中得到了廣泛的套用。

四元式

四元式實際上是一種“三地址語句”的等價表示。它的一般形式為：

(op,arg1,arg2,result)

其中， op為一個二元 (也可是一元或零元)運算符；arg1,arg2分別為它的兩個運算 (或操作)對象，它們可以是變數、常數或系統定義的臨時變數名；運算的結果將放入result中。四元式還可寫為類似於PASCAL語言賦值語句的形式：

result ∶= arg1 op arg2

需要指出的是，每個四元式只能有一個運算符，所以，一個複雜的表達式須由多個四元式構成的序列來表示。例如，表達式A+B*C可寫為序列

T1∶=B*C

T2∶=A+T1

其中，T1，T2是編譯系統所產生的臨時變數名。當op為一元、零元運算符 (如無條件轉移)時，arg2甚至arg1應預設，即result∶=op arg1或 op result ；對應的一般形式為：

(op,arg1,,result)

或

(op,,,result)

在實際產生的四元式中，op往往用一整型數表示 (操作符的代碼)，它可能附帶有不止一種屬性。例如，加運算可以分為定點加法和浮點加法兩種，我們可用不同的整數值區分這兩種加法。至於四元式中運算對象arg1、arg2和結果域result，它們可以是指向符號表中某項的指示字，也可以是某個臨時變數的序號，因此，在實際的翻譯過程中，還需要進行相應的查填符號表工作。在本章中，由於我們只作原理性討論，所以假定臨時變數來自一個用之不竭的集合，而不去追求其經濟性。

三元式

為了節省臨時變數的開銷，有時也可採用一種三元式結構來作為中間代碼，其一般形式為：

○i(op,arg1,arg2)

其中，○i為三元式的編號，也代表了該三元式的運算結果；op,arg1,arg2的含義與四元式類似，區別僅在於arg可以是某三元式的序號，表示用該三元式的運算結果作為運算對象。例如，對於賦值語句

a∶=-b*(c+d)

若用三元式表示，則可寫成

①(Uminus, b, - )

②( + , c, d )

③( * , ①, ② )

④( ∶= , a, ③ )

式①中的運算符Uminus表示一元減運算。

下面，我們仍以算術表達式到三元式的翻譯為例，說明如何為各產生式設計語義動作。為此，先定義翻譯過程中要使用的若干輔助函式：

int LookUp(char*Name)——以Name (變數名)查符號表，若查到則返回相應登記項的序號(≥1)，否則，返回0。

int Enter(char*Name)——以Name為名字在符號表中登錄新的一項，返回值為該項的序號。

int Entry(char*Name)——以Name為名字查、填符號表，即

int Entry(char*Name)

{ int i=LookUp(Name);

if(i) return i;

else return Enter(Name);

}

注意，在實際的編譯系統中，還應區分當前是否在處理說明部分：若是說明部分，則查表時i應為0 (否則Name被重複定義)；若非，則i不能為0(否則Name尚未被定義)。

int Trip(int op,int arg1,int arg2)——根據給定的參數產生一個三元式

(op,arg1,arg2)

並將它送入三元式表中，其返回值為該三元式在表中序號。為區分參數arg所表示的是三元式編號還是變數，約定當arg<0時表示三元序號；arg>0表示變數在符號表中登記項的序號；arg=0表示參數為空。

利用這些函式，我們可構造將表達式翻譯成三元式的S屬性翻譯文法如下：

1Expr′→Expr{$$=$1;}

2Expr→Expr ′+′ Term{$$=Trip(′+′,$1,$3);}

3|Term{$$=$1;}

4|′-′Term{$$=Trip(Uminus,$2,0);}

5Term→Term′*′Factor{$$=Trip(′*′,$1,$3);}

6| Factor{$$=$1;}

7Factor→ ′(′ Expr ′)′ {$$=$2;}

8| iden{$$=Entry($1);}

在產生式8中，終結符號iden的屬性是它的詞文yytext(其值由LEX所生成的掃描器提供)，用$1表示。每個非終結符號都有一個屬性，代表以該符號為根的語法樹的一個子樹的運算結果，該屬性的取值可以是整型數，或為一個三元式的序號，或為符號表項的序號。

比較三元式和四元式這兩種表示方法可以看出，無論在一個三元式序列還是四元式序列中，各個三元式或四元式都是按相應表達式的實際運算順序出現的。其次，對同一表達式而言，所需的三元式或四元式的個數一般是相同的。不過，由於三元式沒有Result欄位，且不需要臨時變數，故三元式比四元式占用的存儲空間少。另一方面，當進行代碼最佳化處理時，常常需要從現有的運算序列中刪去某些運算，或者需要挪動一些運算的位置，這對於三元式序列來說，是很困難的。因為，三元式間的相互引用一般非常頻繁，而這些引用又是通過其中的指示字來實現的，所以，一些三元式的刪除或挪動，有時會造成需要大量修改指示字內容的局面。但對於四元式序列來說，由於四元式之間的相互聯繫是通過臨時變數來實現的，所以，更改其中一些四元式給整個序列帶來的影響比三元式的情況小得多。

為了克服三元式表示不便於最佳化的缺點，可在中間代碼生成過程中，建立兩個與三元式有關的表格。一個稱為三元式表，用於存放各三元式本身；另一個稱為執行表，它按照各三元式的執行順序，依次列出相應各三元式在三元式表中的編號。也就是說，現在我們用一個三元式表連同執行表來表示中間代碼，通常我們將此種表示方式稱為間接三元式。例如，對於如下賦值語句

x∶=(a+b)*c;

b∶=a+b;

y∶=c*(a+b)

若按三元式表示，可寫成

①(+, a,b)⑤(+, a,b)

②(*, ①,c)⑥(*, c,⑤)

③(∶=, x,②)⑦(∶=, y,⑥)

④(∶=, b,①)

其中，三元式①和⑤形式完全一致，但卻不能將⑤省去；對於②，⑥來說，也應當說是一致的 (因為乘法滿足交換律)，同樣不能將⑥省去。然而若按間接三元式表示，則可寫成

執行表三元式表

①①(+, a, b)

②②(*, ①,c)

③③(∶=,x,②)

④④(∶=,b,①)

①⑤(∶=,y,②)

②

⑤

由此可見，這兩種表示法的區別之一就是，對於間接三元式表示而言，由於在執行表中已經依次列出每次要執行的那個三元式，若其中有相同的三元式，則僅需在三元式表中保存其中之一。這就意味著，三元式表的項數一般比執行表的項數少。

另外，當進行代碼最佳化需要挪動運算順序時，則只需對執行表進行相應的調整，而不必再改動三元式表本身。這樣，就避免了前述因改變三元式的順序所引起的麻煩。