啟發式程式是實現啟發式搜尋算法的電腦程式。著名的啟發式搜尋程式有20世紀70年代初N.J.尼爾松給出的A算法、A’算法,以及後來的與或圖啟發式AO‘搜尋算法等。
基本介紹
- 中文名:啟發式程式
- 外文名:heuristic procedure
- 拼音:qǐ fā shì chéng xù
- 定義:實現啟發式搜尋算法的電腦程式
- 性質:局域性、試探性、針對性
- 套用學科:程式語言術語
概述
性質
啟發式程式的套用環節
知識表示





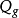


搜尋求解
啟發式搜尋策略




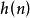



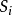
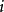



啟發式程式是實現啟發式搜尋算法的電腦程式。著名的啟發式搜尋程式有20世紀70年代初N.J.尼爾松給出的A算法、A’算法,以及後來的與或圖啟發式AO‘搜尋算法等。





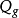






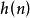



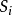
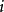


啟發式程式是實現啟發式搜尋算法的電腦程式。著名的啟發式搜尋程式有20世紀70年代初N.J.尼爾松給出的A算法、A’算法,以及後來的與或圖啟發式AO‘搜尋算法等。....
啟發式軟體(Heuristic Software ):通過監控使用者與系統的相互作用,記憶使用者及其使用過程中的知識的軟體解決方案。...
啟發式規則就是基於啟發式的規則,重點在於特徵值識別技術上的更新、解決單一特徵碼比對的缺陷。目的不在於檢測所有的未知病毒,只是對特徵值掃描技術的補充。...
啟發式:英文Heuristic;簡化虛擬機和簡化行為判斷引擎的結合。主要針對:木馬、間諜、後門、下載者、已知病毒(PE病毒)的變種。...
啟發式方法指人在解決問題時所採取的一種根據經驗規則進行發現的方法。其特點是在解決問題時,利用過去的經驗,選擇已經行之有效的方法,而不是系統地、以確定的步驟...
啟發式分析是一種為計算機軟體做可用性檢查的方法,以找出在UI設計時存在的可用性的相關問題。啟發式分析一般是由一到三個分析員來執行,主要是對UI進行檢查,發現其...
啟發式引擎是基於特徵值掃描技術上的升級,與傳統反病毒特徵值掃描技術相比,優點在於對未知病毒的防禦。是特徵值識別技術質的飛躍。...
啟發式掃描技術,實際上就是把這種經驗和知識移植到一個查病毒軟體中的具體程式體現。因此,在這裡,啟發式指的“自我發現的能力”或“運用某種方式或方法去判定事物...
算法一啟發式理論是學習與教學心理學理論。俄羅斯心理學家蘭達20世紀60年代初創立。該理論認為,要形成和發展學生的解題能力,就必須讓學生掌握問題解決的合理思維方法...
啟發式教學是指教師在教學過程中根據教學任務和學習的客觀規律,從學生的實際出發...這種理論,是近代教育史上,首先明確地把教學的過程分為有計畫的程式,即“明了...
啟發式防毒就是把這種經驗和知識移植到一個查病毒軟體中的具體程式體現。...... 啟發式防毒就是把這種經驗和知識移植到一個查病毒軟體中的具體程式體現。...
啟髮型病毒肯定式啟發 一種檢測規則或標準,如果檢測對象符合標準,則是病毒或惡意軟體的可能性加大。啟髮型病毒誤殺漏殺原因 編輯 爭論的焦點在於,判斷一個程式是不...
《不確定狀態下的判斷啟發式和偏差》是2008年9月1日中國人民大學出版社出版的圖書,作者是卡尼曼。...
啟發式知識是實現啟發式搜尋算法的計算機程式。著名的啟發式搜尋程式有20世紀70年代初N.J.尼爾松給出的A算法、A’算法,以及後來的與或圖啟發式AO‘搜尋算法等。....
啟發式搜尋策略即為結點排序技術。α-β 搜尋/剪枝算法的剪枝效率對同一結點下的孩子結點的排列順序非常敏感,這些結點的排列越理想,則剪枝越早發生,需要展開和估值...
程式設計與實踐(VB.NET)》是將啟發式教學方法變成可操作的教學方法。...... 程式設計與實踐(VB.NET)》是將啟發式教學方法變成可操作的教學方法。ISBN 9787121156236...
選擇程式設計難點 1)理解選擇結構語句執行的邏輯過程;2)如何運用選擇結構解決實際編程問題;選擇程式設計教學策略 編輯 本課綜合運用講授法、啟發式、自主學習、協作...
對於大型程式,也可以是這三種結構的混合。軟體結構WEB軟體結構原則 軟體結構軟體結構設計的啟發式規則 (1)模組功能的完善化執行規定功能部分;出錯處理部分;需返回給...
為了完成這些任務,需要採用符號信息處理、啟發式程式設計、知識表示、自動推理和決策等有關技術。隨著人工智慧和計算機技術的發展,已經有可能把自動控制和人工智慧以及...
啟發式防毒是小紅傘的最大特點,這裡有必要介紹一下啟發式防毒:病毒程式與正常的套用程式在啟動時有很多區別,有些非常明顯的區別可以被發現,例如:通常一個套用程式在...
