基本介紹
- 中文名:向後選擇法
- 外文名:backward elimination
- 所屬學科:數學
- 別名:向後剔除法、向後消元法
- 所屬問題:數理統計
- 相關概念:向前選擇法,逐步回歸法等
- 簡介:一種回歸模型的自變數選擇方法
基本介紹,基本過程,
基本介紹
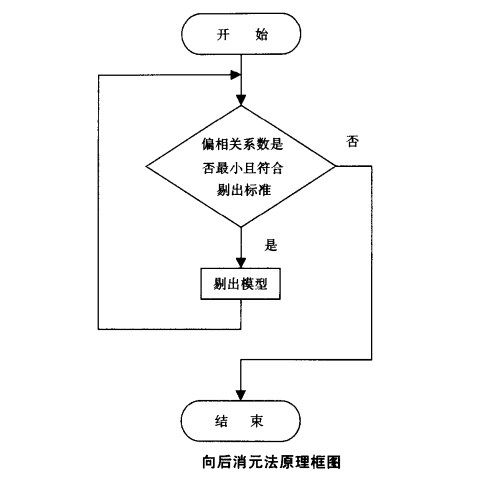
從所有變數一次加入回歸方程開始,然後按順序剔除對回歸方程影響不顯著的變數,這種篩選自變數的方法稱為向後選擇法,也稱向後剔除法、向後消元法。向後消元法是一種其特點與向前選擇法恰好相反的回歸分析方法,它從模型中包含所有的備選自變數開始。一個備選自變數如果與因變數的偏相關係數是最小的,且其F值小於“剔出標準”,則被剔出模型。下一個被剔出模型的自變數是在剩餘的自變數中偏相關係數最小,且其F值小於“剔出標準”的備選自變數。這種疊代過程一直進行下去,直到再也沒有備選自變數符合“剔出標準”為止。一旦一個變數被從模型中剔出,它就不能在下一步再重新進入模型。
向後消元法的SPSS操作要在Method:下拉選框中選中Backward(向後消元法)選項,其餘的操作與逐步回歸法和向前選擇法基本相同。
剔除變數的判別標準為:①F移出法標準FOUT:當F統計量值<FOUT(臨界值,SPSS中內定此值為2.71)時,變數移出回歸方程;②F最大機率移出標準FOUT:當F統計量的相伴機率>FOUT(臨界值,SPSS中內定此值為0.1)時,變數從回歸方程中移出。向後剔除法是從全部變數均在回歸方程中開始,然後每次剔除一個F統計量的相伴機率最大且符合上述標準①或②的變數,直至留在方程中的變數再也沒有達到剔除標準時為止。最後一個回歸方程,即為最優的回歸方程。
基本過程
與向前選擇法相反,其基本過程如下:
1.先對因變數擬合包括所有k個自變數的線性回歸模型。然後考察p(p<k)個去掉一個自變數的模型(這些模型中的每一個都有k-1個自變數),使模型的SSE值減小最少的自變數被挑選出來並從模型中剔除。
2.考察p-1個再去掉一個自變數的模型(這些模型中的每一個都有k-2個自變數),使模型的SSE值減小最少的自變數被挑選出來並從模型中剔除。如此反覆進行,一直將自變數從模型中剔除,直至剔除一個自變數不會使SSE顯著減小為止。這時,模型中所剩的自變數都是顯著的。上述過程可以通過F檢驗的P值來判斷。