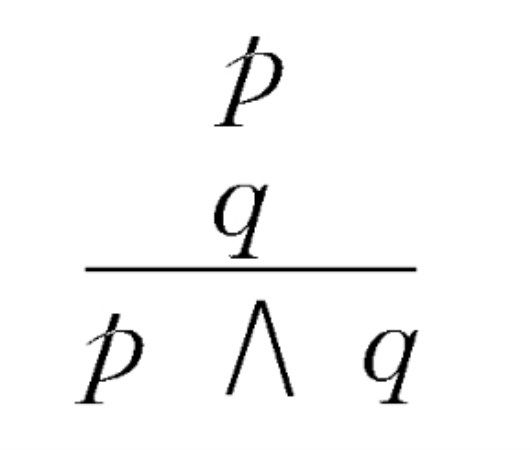合取引入規則(introduction rule of conjunction)是推理規則的一種,如果前提p為真,q為真,則得結論p與q為真,即p∧q為真,由此可得推理規則,這個推理規則稱為合取引入規則。
基本介紹
- 中文名:合取引入規則
- 外文名:introduction rule of conjunction
- 所屬學科:邏輯學
- 簡介:某些自然推理系統中的推理規則
基本介紹,例題解析,
基本介紹
合取引入規則是某些自然推理系統中的推理規則之一。簡記為∧Ⅰ。可表述為兩種形式:
(1)若Γ├A且Δ├B,則Γ∪Δ├A∧B;
(2)若Γ├A且Δ├B,Γ∪Δ├B∧A。
其中Γ和Δ是任意的公式的集合,A、B是公式,├是推出關係。這一規則意為:
若Γ可以推出A,並且Δ可以推出B,則Γ和Δ的並集可以推出A與B的合取式A∧B和B∧A。
這一規則又可用如下的圖式來表示:

也可以表述為如下的圖式:

例題解析
【例1】設已知前提為

證明








【例2】有張、王、李、趙四人均為同班同學,有如下的事實:如張與王去看球賽則李也一定去看;現有張去看球賽或趙不去看球賽;王去看球賽。此時有結論:如趙去看球賽則李也去。試用蘊涵推理方法求證此結論。
解 設命題:
P:張看球賽;
Q:王看球賽;
R:李看球賽;
S:趙看球賽。
此時有前提:

證明