古德曼函式(Gudermannian function)是一個函式。它無須涉及複數便將三角函式和雙曲函式連繫起來。
基本介紹
- 中文名:古德曼函式
- 外文名:Gudermannian function
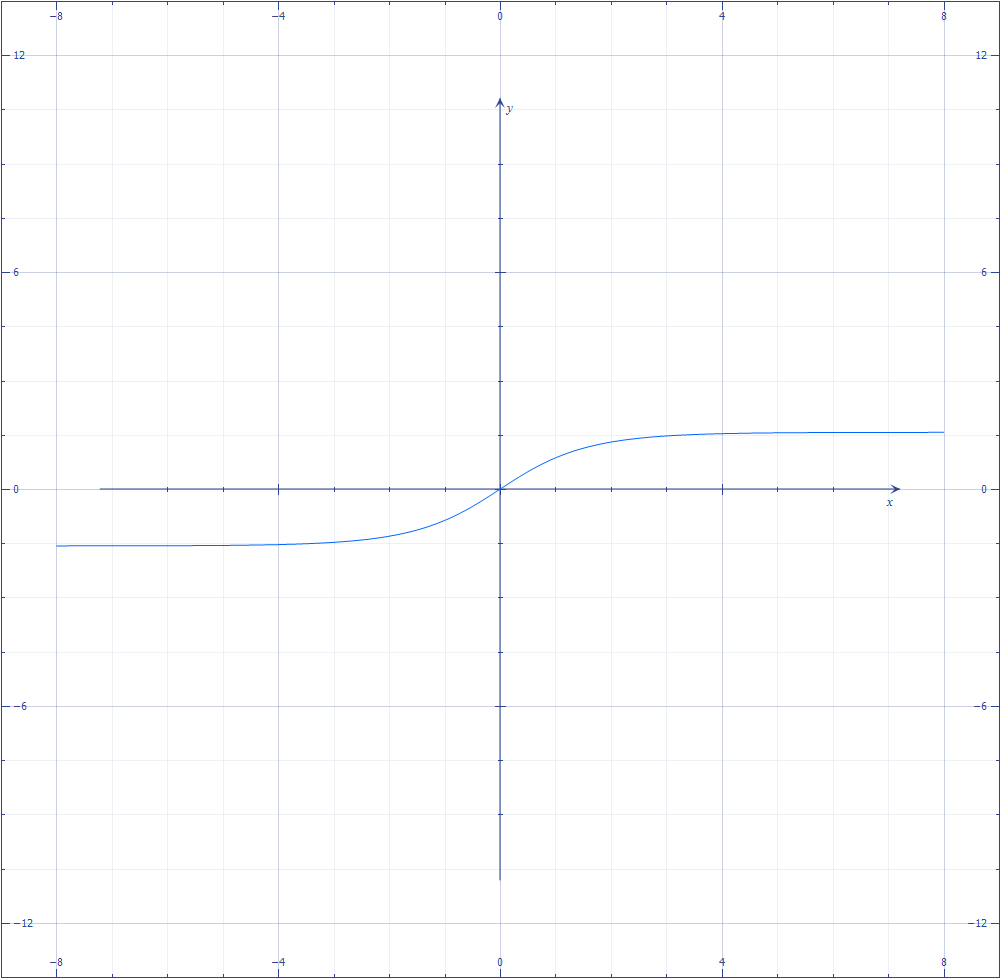
古德曼函式(Gudermannian function)是一個函式。它無須涉及複數便將三角函式和雙曲函式連繫起來。

古德曼函式(Gudermannian function)是一個函式。它無須涉及複數便將三角函式和雙曲函式連繫起來。gd(x)=∫(上x下0)dt/cosht=2arctan(e^x)-π/2有以下恆等式:sin(gd(x...
古德曼函式(Gudermannian function)是一個函式。古德曼函式,它無須涉及複數便將三角函式和雙曲函式連繫起來。gd(x)=∫(上x下0)dt/cosht=2arctan(e^x)-π/2 有以下恆等式:sin(gd(x))=tanh(x)cos(gd(x))=sech(x)t...
創立“古德曼函式”。他十分重視函式的級數展開式的研究,他的學生魏爾斯特拉斯在這些成果的基礎上發展了函式理論。古德曼還編制了雙曲線函式表。在幾何學中,他首先提出球面圓錐曲線表。古德曼的著作主要有《球面解析概論》(1830)、《模...
第四節 凹函式、凸函式和?效用函式?第二章 風險、風險厭惡與隨機占優 第一節 風險與風險偏好 第二節 隨機占優?附錄?第三章均值方差證券投資組合選擇模型風險和收益的數學度量 第一節 風險和收益的數學度量 第二節 馬克維茨模型的...
11.3用this向函式傳遞元素 146 11.4提交和預驗證表單 149 11.5習題 152 第12章String、Math和Date對象 155 12.1核心語言對象 155 12.2String對象 155 12.2.1連線字元串 156 12.2.2字元串方法 157 12.3Math對象 159 12.4...
內容涉及二維信號和系統的分析、標量衍射理論基礎、菲涅耳衍射與夫琅禾費衍射、計算衍射和計算傳播、相干光學系統的波動光學分析、光學成像系統的頻譜分析、點擴展函式和傳遞函式的工程、波前調製、模擬光學信息處理、全息術、光通信中的傅里...
4.6.3 積分強度的機率密度函式的“準確”結果 4.6.4 部分偏振散斑圖樣的積分 4.7 散斑強度和相位的微商的統計性質 4.7.1 背景 4.7.2 各種散射光斑形狀下的參數 4.7.3 散斑相位的微商:散斑圖樣中的光線方向 4.7.4...
9.3 Win32中的Global和LocalAlloc函式 9.4 用標準C語言庫管理記憶體 9.5 在Win32的下新堆API 9.5.1 用於分配更大記憶體的HeapRealloc 9.5.2 撤消堆的HeapDestroy 9.5.3 MFC C++ new及delete函式 結構異常處理 9.6 管理記憶體...
