反應堆內，中子的產生率和消失率之間保持嚴格的平衡，使鏈式反應得以恆定的速率持續地進行下去的工作狀態。具有給定幾何布置與材料組成的堆芯或裝置能夠達到臨界所需的最小尺寸，稱為臨界尺寸或臨界大小。臨界反應堆核心燃料的裝載量，也就是維持自持鏈式裂變反應所需的易裂變物質的最小質量稱為臨界質量。一座反應堆的臨界質量通常指反應堆芯部中沒有控制棒和化學補償毒物情況下的臨界質量。反應堆的臨界質量取決於反應堆的類型、材料成分、幾何形狀和結構等條件，但對於任何一個特定的反應堆系統，它是一個確定的數值。例如，用235U作燃料的反應堆，其臨界質量可以小於1kg，大到200kg。前者是含有235U富集度為90%左右的鈾鹽溶液系統的臨界質量，後者是天然鈾石墨反應堆中所含的235U質量。反應堆的臨界條件可以通過增殖因數來表示。
基本介紹
- 中文名：反應堆臨界
- 外文名：criticality of reactors
增殖因數,臨界計算,分群擴散法,
增殖因數
反應堆中新生一代的中子數與產生它的直屬上一代中子數之比，或中子的產生率與中子的消失率之比，通常用符號k表示。在反應堆系統內，中子主要是由於易裂變物質的裂變反應產生的。中子的消失有兩種途徑，即在反應堆內被吸收和從反應堆表面泄漏出去。增殖因數又分為無限增殖因數和有效增殖因數。
(1)無限增殖因數：假想的無限大增殖介質的增殖因數，通常用k∞表示。對於無限大系統，沒有中子泄漏損失，中子由核裂變產生，並且僅由於被系統內各種材料的吸收而損失。熱中子反應堆的無限增殖因數可用k∞=fηεp表示，其中f為熱中子利用因數，它是被增殖介質內所有材料吸收的熱中子中，為燃料所吸收的份額；η是燃料每吸收一個熱中子後由於裂變而釋放的快中子平均數；ε是快裂變因子，它是每一初級裂變中子所得到的最後慢化到U裂變閾能以下的中子數；p為逃脫共振吸收機率，它表示中子在慢化過程中逃脫共振吸收的份額。k∞=fηεp稱為四因子公式，它是反映系統材料增殖特性的重要參數。四因子模型在早期熱中子反應堆的計算與分析中被廣泛地套用。
(2)有效增殖因數：有限大反應堆系統的增殖因數，通常用keff表示。對有限大系統必須考慮中子的泄漏損失，根據定義， keff =k∞Λ，其中k∞為無限增殖因數； Λ為系統的中子不泄漏機率，它由兩部分組成:慢化過程中的不泄漏機率Λs和熱中子擴散過程中的不泄漏機率Λd即Λ=ΛsΛd。不泄漏機率不僅與系統的材料特性，也與系統的大小和幾何形狀有關。因而，在沒有外中子源時，有限大反應堆系統的臨界條件是keff =1，這時反應堆處於穩態，反應堆內中子有一個穩定的分布。若keff<1，則系統是次臨界的，當沒有外中子源時，中子注量率就會不斷衰減到零。若keff>1，系統是超臨界的，中子注量率將隨時間不斷地按指數規律增長。圖中給出了熱中子反應堆內的中子平衡關係。
熱中子反應堆內中子平衡示意圖
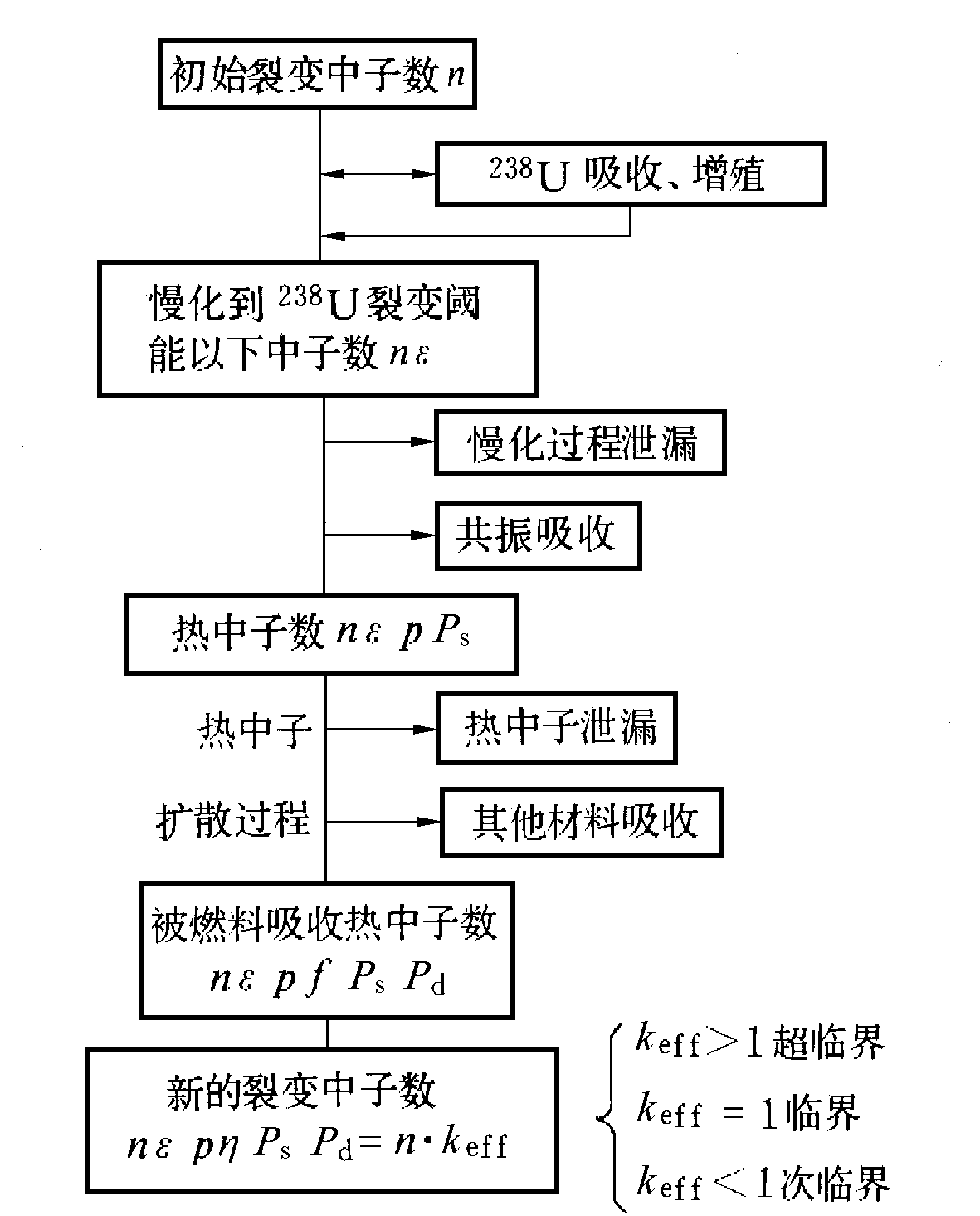熱中子反應堆內中子平衡示意圖臨界計算
反應堆臨界計算的任務可以歸納為以下幾類問題:①給定了反應堆的材料成分，確定它的臨界尺寸。②給定反應堆的形狀和尺寸(對於動力反應堆，通常由反應堆熱工計算確定)，確定臨界時反應堆的材料成分。一般是確定燃料的U富集度，或所需控制毒物的數量及其布置。這是工程設計中常遇到的情況。③在反應堆物理設計及燃耗計算中，還經常遇到這樣一類問題，可稱之為臨界性計算，即反應堆的幾何形狀、大小以及芯部的燃料和其它材料成分都已給定，需要求出反應堆的有效增殖因數或反應性。
臨界計算是反應堆物理設計的重要部分，除了求出反應堆臨界時的體積大小和燃料成分及燃料裝載量外，另一個重要的任務是確定臨界狀態下系統內中子注量率的分布。而堆芯內的釋熱率或功率的分布是和中子注量率分布成比例的。
反應堆臨界計算常用的方法有:連續慢化理論和分群擴散理論。
分群擴散法
研究多能中子擴散的一種近似方法。它是計算帶有反射層或多區反應堆的有效和常用方法。在這種處理方法中，將中子能量自裂變中子上限能量到熱能之間分成為若干個能量區間，或者叫做“能群”。同一能群中子的擴散、散射和吸收用適當平均後的群參數和群截面(稱為“群常數”)來描述，各群中子的輸運行為用能群擴散方程表述。在這種分群理論中，最簡單的是“單群”理論，但是它只能給出比較近似的結果。在熱中子反應堆計算中，尤其對於以石墨或重水為慢化劑的反應堆，常常採用兩群擴散理論。這時，只要群常數選取得當，就能給出比較好的結果。但是近年來隨著計算技術的發展及新的堆型(如快中子反應堆)的出現以及對反應堆計算提出更高的要求，則採用少群(2~4群)或多群理論進行計算。
(1)中子注量率分布 在臨界狀態時， 反應堆內的中子具有穩定的空間分布。 它滿足波動方程▽j(r)+Bj(r)=0，其中，B為方程的本徵值，j(r)為中子注量率空間分布。可以證明，在臨界時中子注量率將達到一個穩定分布，它只取決於基態(n=1)的最小本徵值，其他所有模態(n>1)都衰減了。用B g表示基態的本徵值B 1，通常稱為系統的幾何曲率。幾何曲率和反應堆的幾何形狀以及尺寸有關。表中給出不同形狀裸堆的幾何曲率和中子注量率分布。
各種幾何形狀裸堆的幾何曲率和中子注量率分布見表。
幾何曲率和中子通量密度分布
幾何形狀 | 尺 寸 | 幾何曲率 | 中子通量密度分布 |
球形(r) | 半徑R | A= | |
長方體(x，y，z) | 邊長a，b，c | ||
圓柱體(r、z) | 半徑R高度H | AJ0 |
* 包括外推距離。
實際上，在反應堆堆芯外圍都設有反射層。反射層是將從反應堆堆芯逃逸出的中子部分散射回反應堆堆芯的結構。反射層的存在可在不改變反應性的條件下減小該堆芯給定方向上的尺寸，即減少臨界質量。
(2)熱中子注量率不均勻係數 反應堆堆芯內熱中子注量率的最大值與堆芯內熱中子注量率的平均值之比，通常以Fq表示。堆芯內某一點發出的功率是與該點的核裂變反應率Σfφ成正比的。當各點巨觀裂變截面為常數時，功率分布是與中子注量率分布成正比的。Fq愈大，堆芯內功率分布愈不均勻。所以，Fq是表征堆芯內熱中子注量率分布不均勻程度的一個物理量。對於圓柱形裸堆，Fq可以分離成徑向中子注量率不均勻係數FR和軸向中子注量率不均勻係數FZ，即Fq=FRFZ。對於不同形狀裸堆，利用表中的中子注量率分布函式可求出Fq值:球形裸堆，Fq=3.27；圓柱形裸堆，FR=2.31，FZ=1.57，Fq=3.63；正方形裸堆，Fq=3.88。
對於給定的反應堆，單位體積的最大允許功率輸出受到熱工條件的限制。因此，為了提高堆芯總的功率輸出，必須採取一些措施使得反應堆內中子注量率分布變得平坦一些，通常稱為注量率展平。注量率展平的主要措施有:①反應堆堆芯核燃料分區布置，將堆芯按徑向分布為若干區，每一區採用不同富集度的燃料，這樣可以達到徑向展平的目的。②在壓水堆中，採用化學補償溶液控制減少控制棒的數目與提升和下插的次數，減少功率的擾動。③控制棒與可燃毒物的合理布置。此外，反應堆堆芯外的反射層也起展平中子注量率密度分布的作用。
(3)臨界方程 表示反應堆達到臨界，維持自持鏈式反應的條件。上述keff=k∞ΛL=1為臨界條件。用不同的理論，可以求得關於不泄漏機率的不同表達式。年齡理論的熱中子裸堆的臨界方程為=1，單群理論為=1，而兩群理論則為=1，其中L為熱中子擴散長度； τ為中子年齡； 或 1/(1+τB)是慢化過程的不泄漏機率Λs；1/(1+LB)為熱中子擴散過程的不泄漏機率Λd；B為反應堆的幾何曲率。
通常把滿足上述臨界方程的B值稱為材料曲率，記為Bm。材料曲率Bm顯然只取決於增殖系統的材料成分和特性(如，k∞，L，τ等)，而與系統的幾何形狀及大小無關。例如，對於單群理論，。引進了材料曲率概念後，反應堆臨界條件可簡述為：臨界時，材料曲率等於幾何曲率，即臨界方程可以寫成Bg=Bm。
(4)柵格的非均勻效應 由於柵格結構的非均勻性，引起燃料和慢化劑內的中子注量率分布不同，並使反應堆物理參數發生變化的效應。非均勻熱中子反應堆中，核燃料按規則或周期方式排列，呈柵格結構。在非均勻柵格中，由於燃料塊空間自屏效應，燃料塊內的熱中子注量率比慢化劑中的低，使得熱中子利用係數減小。另一方面，由於空間自屏效應，燃料內共振中子注量率降低，同時由於在非均勻結構內，中子在慢化過程中與慢化劑核碰撞的機率增大，減少了燃料對共振中子的吸收，而使逃脫共振機率增加。這是非均勻堆的一個主要優點。此外，非均勻結構增加了裂變中子與U核發生快中子裂變反應的機率，使快裂變因子比均勻堆的大。通過合理地選擇燃料元件的尺寸和燃料元件間的距離(柵距)，在燃料與慢化劑核數比值相同的情況下，可使非均勻柵格的k∞比均勻反應堆的大。例如，在1942年前後，當時只有天然鈾可用作核燃料。分析表明，由天然鈾與即使吸收性能很小的慢化劑，如石墨和重水，所組成的均勻系統是無法使k∞大於或等於1，達到臨界的。但是，稍後進一步分析表明，若將天然鈾和石墨組成非均勻系統是可以達到臨界的。這就是為什麼世界上建成的第一座反應堆是非均勻的原因。
在計算非均勻反應堆時，必須考慮柵格的非均勻效應。通常分兩步進行：①計算非均勻柵格的物理參數，在計算時必須考慮到非均勻效應的影響。然後把非均勻反應堆等效成等價的均勻反應堆，這稱之為均勻化過程。②套用均勻反應堆的理論對等效均勻反應堆進行臨界計算。
