反共振

現象介紹

在耦合振盪器的物理學中，類似於共振，伴隨著其振盪階段的大的偏移，反共振是振盪器在特定頻率的振幅中是顯著的最小值。這種頻率被稱為系統的反共振頻率，並且在這些頻率的地方，振盪幅度可以下降到幾乎為零。反共振是由破壞性干擾引起的，例如在外部驅動力和與另一個振盪器的相互作用之間。

反共振可以發生在所有類型的耦合振盪器系統中，包括機械，聲學，電磁和量子系統。它們在複雜耦合系統的表征中具有重要的套用。

對於兩個自由度的強迫振動，當激振力的頻率為某一值時，會出現一個振動靜止的反共振現象，這種反共振現象可以避免機器及結構物共振動的發生。

系統作受迫振動時，如激勵頻率有任何微小變化都會使系統的回響增加的現象，如外加力的頻率有任何微小改變都會引起策動點速度的增加，也就是頻率恰使策動點阻抗的絕對值為極大時，這時稱為物體或系統與外加力發生速度反共振。

發生反共振的最簡單的系統是耦合諧波振盪器的系統，例如擺線或RLC電路。

考慮強度為g的耦合在一起的兩個諧波振盪器，以及由振盪外力F驅動的一個振盪器。這種情況被描述為耦合的常微分方程：

其中w_i表示兩個振盪器的共振頻率和γ_i它們的阻尼率。將變數更改為複數參數

允許我們將它們寫成一階方程：

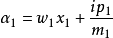
我們在驅動器和振盪器的共振頻率之間引入了失真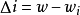

。最後，我們進行旋轉波近似，忽略與e^2iwt成比例的快速反向旋轉項，在我們感興趣的時間尺度上平均為零（這個近似假定，這個近似假設是對於圍繞著周圍的小頻率範圍是合理的）。因此我們得到：

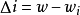
沒有阻尼，驅動或耦合，這些方程的解是

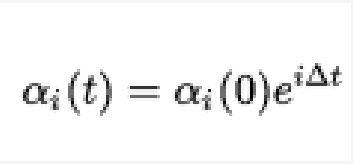
它們表示具有角頻率△的複數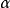

平面中的旋轉。

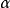
穩態解可以通過設定

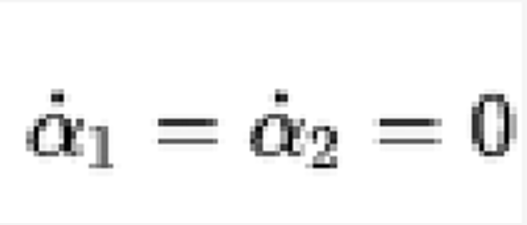
它給出：

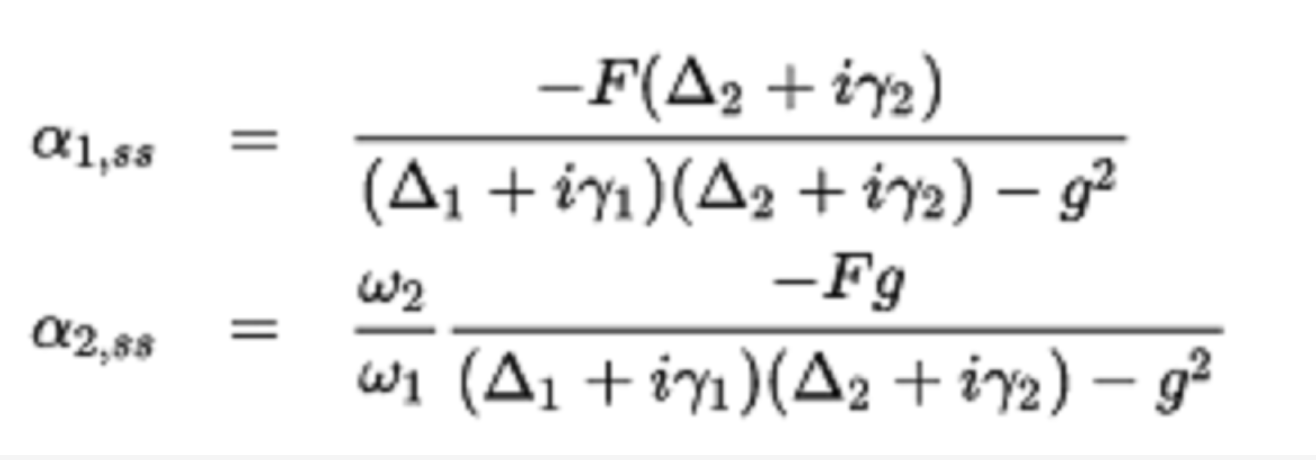
將這些穩態解作為驅動頻率的函式，顯然兩個振盪器在兩個正常模式頻率下顯示共振（振幅峰值伴隨正相移）。此外，驅動振盪器在正常模式之間顯示明顯的幅度下降，伴隨著負相移，這是反共振。請注意，未驅動振盪器的頻譜沒有反共振; 儘管其振幅在正常模式之間具有最小值，但沒有明顯的下降或負相移。

反諧振時的振盪振幅降低可以被認為是由於作用在振盪器上的力的破壞性干擾或抵消。

在反諧振頻率下，作用在振盪器1上的外部驅動力F抵消通過耦合到振盪器2的作用力，使得振盪器1幾乎保持靜止。

具有幾個自由度的動力系統的頻率回響函式的例子，在振幅和相位上都顯示出不同的共振 - 反共振行為。

由許多耦合元件構成的任何線性動態系統的頻率回響函式（FRF）一般會在驅動時顯示出特徵性共振 - 反共振行為。

根據經驗，可以說，隨著驅動部件和測量部件之間的距離增加，FRF中的反諧振次數減少[2]例如，在上述雙振盪器情況下，未驅動振盪器的FRF不顯示反諧振。共振和反共振在驅動部件本身的FRF中不斷交替。