原子公式(數理邏輯)

在數理邏輯中，原子公式（Atomic formula）或原子是沒有子公式的公式。把什麼公式當作原子依賴於所使用的邏輯。例如在命題邏輯中，唯一的原子公式是命題變數。原子是在邏輯系統中"最小"的公式。在邏輯系統中的合式公式通常通過識別所有有效的原子公式，和給出從兩個原子公式建立公式的規則而遞歸的定義。

基本介紹

• 中文名：原子公式
• 外文名：Atomic formula
• 學科：計算機科學、離散數學
• 定義：邏輯系統中“最小”的公式
• 有關術語：合式公式、謂詞邏輯
• 套用：資料庫系統、計算機輔助製造

概述

在離散數學中，設R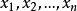（）是Γ的任意n元謂詞，t1,t2,…,tn是任意F的任意的n個項，則稱R（t1,t2,…tn）是Γ的原子公式。通常，原子公式由若干謂詞符號和項組成，常量符號是最簡單的的項，用來表示域內的物體或實體，它可以是實際的物體，也可以是概念或有名字的事情，變數符號也是項，它不必涉及是哪一個實體。在邏輯系統中的合式公式通常通過識別所有有效的原子公式，和給出從兩個原子公式建立公式的規則而遞歸的定義。從原子公式製作的公式是複合公式。

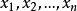
例如，在命題邏輯中有如下的公式構造規則:

任何命題變數 p 是合式原子公式。

給定任何公式 A，否定 ¬A ("非 A") 是合式公式。

給定任何兩個公式 A 和 B，合取 A ∧ B ("A 與 B") 是合式公式。

給定任何兩個公式 A 和 B，析取 A ∨ B ("A 或 B") 是合式公式。

給定任何兩個公式 A 和 B，蘊涵 A ⇒ B ("A 蘊涵 B ") 是合式公式。

所以，我們可以建造任意的複雜的複合公式，比如，從簡單的原子公式p、q 和 r 和我們的構造規則構造出 ((p ∧ ¬(q ⇒ r)) ∨ ¬p)。

謂詞邏輯

簡介

在數學斷言、電腦程式以及系統規格說明中經常可以看到含有變數的語句，例如語句“x大於3”，謂詞就是“大於3”，謂詞表明語句的主語具有的一個性質。

謂詞邏輯是一種邏輯模式，是迄今為止能表達思維和推理的最精確方法，是最廣泛使用的知識表達方式。謂詞邏輯的基本組成部分是謂詞符號、變數符號和常量符號，並用圓括弧、方括弧、花括弧和逗號隔開，以表示域內的關係。也可以稱之為一階邏輯。謂詞邏輯也分為經典的謂詞邏輯和非經典的謂詞邏輯，後者包括作為子系統的非經典的命題邏輯。經典的一階謂詞邏輯是謂詞邏輯的基本部分。第一個完整的謂詞邏輯系統是G.弗雷格在1879年建立的。K.哥德爾等人系統地研究了謂詞邏輯的元邏輯問題，證明了重要的定理。

在謂詞邏輯中，使用量詞應注意以下幾點：

(1) 在不同個體域中，命題符號化的形式可能不同，命題的真值也可能會改變。

(2) 在考慮命題符號化時，如果對個體域未作說明，一律使用全總個體域。

(3) 多個量詞出現時，不能隨意顛倒它們的順序，否則可能會改變命題的含義。

謂詞公式只是一個符號串，沒有什麼意義，但我們給這個符號串一個解釋，使它具有真值，就變成一個命題.。所謂解釋就是使公式中的每一個變項都有個體域中的元素相對應。

在謂詞邏輯中，命題符號化必須明確個體域，無特別說明認為是全總個體域。一般地，使用全稱量詞"，特性謂詞後用®；使用存在量詞$，特性謂詞後用&Ugrave；

公理系統

謂詞邏輯的普遍有效的公式為數無窮，在一定意義上它們都是邏輯規律。為了系統地研究這類規律,需要對它們作整體的考慮,將它們總括在一個系統之中。謂詞演算或者一階謂詞演算就是這樣的系統。謂詞演算是把謂詞邏輯公理化和形式化而建立的形式系統。按照對作為演算出發點的初始符號、公理和變形規則的不同挑選，可以建立不同的謂詞演算系統。在初始符號中有符號=的，稱為帶等詞的一階謂詞演算，等詞=是一個謂詞常元；不帶等詞的系統就稱為（一階）謂詞演算。構成一個謂詞邏輯的公理系統的基本要素有：初始符號、形成規則、公理和變形規則等。對此，可以從一個不帶等詞的系統 F得到說明。 F的初始符號，包括個體變元、謂詞變元、聯結詞和量詞以及技術性符號四類。個體變元符號的小寫拉丁字母為： x,y,z,x1,y1,z1,x2,…；謂詞變元符號為大寫拉丁字母，即：F,G,H,F1,G1,…。在原則上,對每一n≥1，應分別列出n元謂詞變元，如：F1,G1,H1,…;F 2,G 2,H 2,…；等等。不過,省去上標1,2,…,n，在實踐上不會產生混亂。聯結詞和量詞符號為：塡、→、凬；技術性符號為括弧（，）和逗號，。 　形成規則規定怎樣的符號序列或符號的組合是 F中的合式公式。合式公式經解釋後是有意義的。用來描述和討論 F系統的語言即元語言的符號有：小寫希臘字母α，α1，…,αn，δ表示任意的個體變元；fn表示任意的n元謂詞變元;大寫拉丁字母X,Y表示任意的符號序列。這些符號稱為語法變元。F的形成規則有4條：①如果fn是一n元謂詞變元,α1,…,αn是個體變元，則fn(α1,…,αn)是一合式公式；

②　如果 X是合式公式，則塡X是合式公式。如果X、Y 是合式公式，則(X→Y)是合式公式；

③　如果X是合式公式，α是個體變元，則(凬α)X是合式公式；

④　只有適合以上①～③的是合式公式。合式公式簡稱公式。用字母A,B,C表示任意的公式。A,B,C也是語法變元，屬於元語言。

合式公式

命題公式是命題邏輯討論的對象，而由命題變項使用聯結詞可構成任意多的複合命題，如P∧Q, P∧Q∨R, P→Q等。問題是它們是否都有意義呢？只有一個聯結詞的命題P, P∧Q, P→Q當然是有意義的。由兩個聯結詞構成的命題P∧Q∨R至少意義不明確, 是先作P∧Q再對R做∨, 還是先作Q∨R再對P作∧呢? P∧Q也有同樣的問題。解決運算次序是容易的, 可像初等代數那樣使用括弧的辦法, 在邏輯運算中也常使用圓括弧來區分運算的先後次序。這樣由命題變項、命題聯結詞和圓括弧便組成了命題邏輯的全部符號。進一步的問題是建立一個一般的原則以便生成所有的合法的命題公式，並能識別什麼樣的符號串是合法的。

在形式邏輯中，證明是有特定性質的WFF序列，而序列中最終的WFF就是要證明的。

合式公式（簡記為Wff）的定義：

1. 簡單命題是合式公式。

2. 如果A是合式公式, 那么A也是合式公式。

3. 如果A、B是合式公式, 那么(A∧B), (A∨B), (A→B)和(AB)是合式公式。

4. 若且唯若經過有限次地使用1.2.3所組成的符號串才是合式公式。

這個定義給出了建立合式公式的一般原則，也給出了識別一個符號串是否是合式公式的原則。

這是遞歸（歸納）的定義。在定義中使用了所要定義的概念，如在2和3中都出現了所要定義的合式公式字樣，其次是定義中規定了初始情形，如1中指明了已知的簡單命題是合式公式。

條件4說明了哪些不是合式公式，而1、2和3說明不了這一點。

依定義，若判斷一個公式是否為合式公式，必然要層層解脫回歸到簡單命題方可判定。

(P∧Q), (P→(P∧Q)),

(((P→Q)∧(Q→R))(P→R))都是合式公式。而P∨Q∨, ((P→Q)→( ∧Q)), (P→Q都不是合式公式, 沒有意義, 我們不討論。

在實際使用中，為了減少圓括弧的數量，可以引入一些約定，如規定聯結詞優先權的辦法，可按，∨，∧，→，的排列次序安排優先的級別，多個同一聯結詞按從左到右的優先次序。這樣，在書寫合式公式時，可以省去部分或全部圓括弧。通常採用省略一部分又保留一部分括弧的辦法，這樣選擇就給公式的閱讀帶來方便。如

(P→(Q∨R))可寫成P→(Q∨R)或P→Q∨R。

(P→(P→R))可寫成P→(P→R)。

命題演算中只討論合式公式, 為方便起見, 將合式公式就稱作公式。