厄爾姆定理是可數既約準素阿貝爾群的結構定理.。
基本介紹
- 中文名:厄爾姆定理
- 外文名:Ulm's Theorem
厄爾姆定理(Ulm's Theorem)可數既約準素阿貝爾群的結構定理.設G為既約準素阿貝爾群.準素阿貝爾群G中兩個無限高度元素的和與差在G中也有無限高度,從而,所有具有無限高度的元素的集合(加上零元)是群G的一個子群,記為G,一般地,若對小於某一序數月的所有序數a,在群G中已經定義了子群Ga,則當月為非極限序數時,就讓在Gp:中具有無限高度的元素(加上零元)所組成的子群為Gp;若月是極限序數,則讓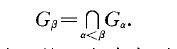
厄爾姆定理
這樣,就可以得到G的一個降序列G=Go>G,>...>Ga> "…由於G的基數不會被超過,所以存在這樣一個序數Y,使得Gr = Gr+,,因此,對所有大於Y的序數}}Gr=Ga.但是等式Gr =Gr+,表明,子群Gr中所有的元素在G,中有無限高度,即子群G,是一個可除群.根據所做假定,群G是既約的,所以子群Gr=0.若:是使Gr =。的最小序數,則稱:為既約準素阿貝爾群的型.若G是一個:型既約準素阿貝爾群,則對所有小於:的序數a,做商群Ga = GalGa+1,群列GO1G,}"..}硯,…,。<:稱為群G的厄爾姆因子列.利用這些概念,可以得到重要的厄爾姆定理:可數既約準素阿貝爾群A和B彼此同構,若且唯若它們有同一型:,且對任何小於:的序數a,它們的厄爾姆因子A。和B。彼此同構.有例子表明厄爾姆定理不能簡單地推廣到不可數的情形,即厄爾姆定理中群的可數性條件是不可少的.
