基本介紹
- 中文名：卡爾松測度
- 外文名：Carleson measure
- 領域：數學
- 涵義：對Rn的子集的一種度量
- 命名：Lennart Carleson
- 套用：諧波分析、偏微分方程理論
簡介,定義,泊松運算元與卡爾松定理,其他相關概念,
簡介
在數學中，卡爾松測度是對維度歐幾里德空間Rn的子集的一種度量。 大致來說，域Ω上的Carleson測量是與Ω邊界上的表面測量值相比，在Ω邊界處不消失的度量。
Carleson測度以瑞典數學家Lennart Carleson命名。Carleson在20世紀60年代早期採用L. Carleson來描述開放單位盤中有界分析函式的代數中的內插序列，並給出了電暈問題的解決方案。
這些措施可以用以下方式定義：讓我們對單位盤
做一個肯定的測量。 那么如果存在一個常數
，那就被稱為Carleson度量，這樣對於每個部分來說都是如此：
Carleson測度在複雜分析、諧波分析、BMO理論、積分運算符理論和等式理論中起著重要作用。
定義
令n∈N，令Ω⊂Rn為非空邊界∂Ω的開放（即可測量）集合。 令μ為Ω上的Borel度量，令σ表示∂Ω上的表面度量。 如果存在常數C> 0，則測量μ被認為是Carleson度量，使得對於每個點p∈∂Ω並且每個半徑r> 0，
其中，
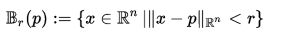
表示半徑r的開放球約p。
泊松運算元與卡爾松定理
令D表示配備有一些Borel測量μ的複平面C中的單位盤。 對於1≤p<+∞，令Hp（∂D）表示D的邊界上的Hardy空間，並且Lp（D，μ）表示D上的Lp空間相對於度量μ。定義泊松運算元：
那么若且唯若測量μ是Carleson時，P是有界線性運算元。
其他相關概念
對於Carleson條件，常數C> 0的集合的最小值：
持有被稱為測量μ的Carleson範數。
如果C（R）被定義為受限Carleson條件的所有常數C> 0的集合的最小值：
如果C（R）→0為R→0，那么測量μ被認為滿足消失的Carleson條件。
