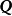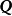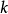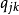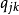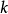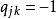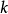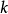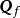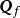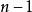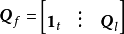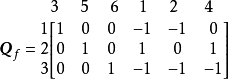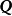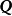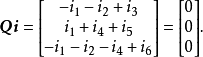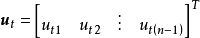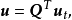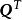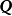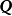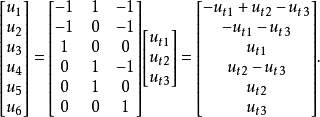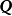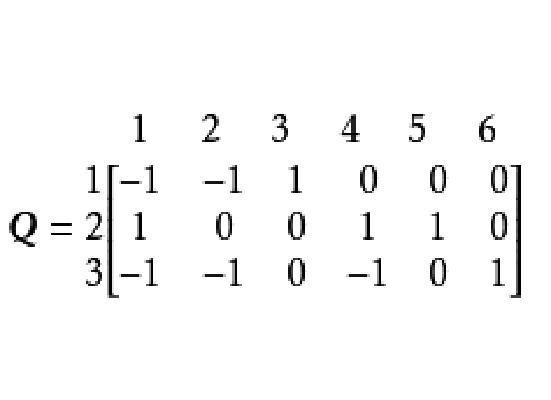割集矩陣

有向圖G中，割集j與支路k的相互關係是：如果支路k不是割集j的元素，則稱支路k與割集j不相關聯；如果支路k是割集j的元素(支路k的方向與割集j的方向可能相同也可能不同)，則稱支路k與割集j相關聯。常用獨立割集矩陣Q (簡稱割集矩陣) 來描述獨立割集與支路的關聯關係。制集矩陣Q的第j行第k列元素用q_jk表示，j為割集序號，k為支路序號，q_jk描述了割集j與支路k的關聯關係。

基本介紹

• 中文名：割集矩陣
• 外文名：cut set matrix 
• 所屬學科：數學
• 所屬問題：圖論
• 相關概念：割集，基爾霍夫定律等

基本介紹

割集是連通圖G中某些支路的集合，若移去這些支路，則連通圖G被分成兩個部分。如果少移去其中的一條支路，圖仍然是連通的。

割集矩陣是描述割集與支路的關聯關係的矩陣。設連通有向圖G有n個結點，b條支路，首先選單樹支割集為獨立割集(規定每個單樹枝割集的方向和樹枝方向相同)，獨立割集數為n-1個，則割集矩陣為一個(n-1)×b階矩陣，用表示。割集矩陣的行和割集對應，列和支路對應，則割集與支路的關聯關係可用它的任一元素表示。取值的具體意義如下：

(1)表示割集與支路關聯，且方向一致。

(2)，表示割集與支路關聯，方向相反。

(3)，表示割集與支路不關聯。

表1

(a)	(b)
(c)	(d)

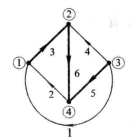
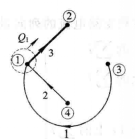
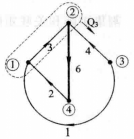
例如，表1(a)所示的獨立割集數為3，如圖1(b)，圖1(c)和圖1(d)所示。其割集矩陣為

和基本迴路類似，如果割集矩陣的列序(割集順序)和樹支所對應基本割集的排序一致，則

這樣的割集矩陣稱為基本割集矩陣，用表示。若割集的方向和對應樹支的方向一致，則中將出現一個階的單位子矩陣，即

式中，下標分別表示與樹支和連支對應的部分。在選定支路3、5、6為樹支，支路1、2、4為連支後，圖1,對應的基本割集矩陣為

用割集矩陣表示的KVL和KCL方程

割集矩陣和關聯矩陣類似，若用矩陣左乘支路電流的列向量，有

即

該式就是用表示的KCL的矩陣方程。

對於圖1(a)所示的圖，若所選獨立割集與圖1所示的相同，則

對於n個結點、b條支路的圖，設n-1個樹支電壓的列向量為

於是，各支路電壓可以用樹支電壓來表示，即

式中為割集矩陣的轉置矩陣。可見，如果已知n-1個樹支電壓，則b條支路的電壓可以用樹支電壓表示，這是割集電壓法的基本思想。該式就是用矩陣表示的KVL的矩陣形式。

例如，圖1所示的支路電壓與其樹支電壓關係的矩陣表示為

由以上分析看出：

(1) KCL和KVL既可以用A矩陣和B矩陣表示，同樣可以用矩陣表示。它們之間存在等效變換關係。當連通圖的A矩陣、B矩陣和矩陣的階次不同時，其KCL和KVL表示式的複雜程度也不同。

(2)KCL、KVL和電路的拓撲結構有關，這是集總元件電路公設的必然結果。對集總電路而言，無論其支路元件是線性的還是非線性的、時變的還是非時變的，基爾霍夫定律總是成立的。

(3)電路是由電路元件組成的。電能在電路中的實際分布不僅受KCL和KVL約束，也要受支路元件特性的約束。只有把元件約束(元件的伏安特性)與基爾霍夫定律相結合，才能確定電路元件上的能量分布，完成電路分析的任務。