切向畸變

“切向畸變”就是矢量端點沿切線方向發生的變化，也就是角度的變化dt。

基本介紹

• 中文名：切向畸變
• 外文名：Tangential distortion
• 表達式：矢量端點沿切線方向發生的變化
• 適用領域範圍：攝影等
• 原因：攝像機製造上的缺陷

概念

切向畸變是由於攝像機製造上的缺陷使得透鏡本身與圖像平面不平行而產生的，可定量描述為：

x_correct=x+(2p₁xy+p₂(r²+2x²))

y_correct=y+(p₁(r²+2y²)+2p₂xy)

式中，（x，y）是畸變點在圖像上的原始坐標，（x_correct，y_correct）是校正後的新坐標，p₁、p₂為切向畸變係數。

帶切向畸變的模型可視化攝像機標定

建立攝像機成像的幾何模型，用以描述空間坐標系中物體點同它在圖像平面上像點之間的對應關係。其幾何模型的參數就是攝像機的參數，計算、求解這些參數的過程稱為攝像機標定。傳統的攝像機定標方法可以分成四類，即利用攝像機變換矩陣的標定方法，利用最最佳化算法的標定方法，進一步考慮畸變補償的兩步法和採用更為合理的攝像機成像模型的雙平面標定方法。

直接線性變換方法或者透視變換矩陣方法可以利用線性方法求解攝像機參數，其缺點是沒有考慮鏡頭的非線性畸變，精度不高；使用最最佳化算法求解未知參數，求解的結果常常取決於給定的初始值。如果初始值給定不合適，就很難得到正確的結果。如果先利用直接線性變換方法或者透視變換矩陣方法求解攝像機參數，再以求得的參數為初始值，考慮畸變因素，並利用最最佳化算法進一步提高標定精度，這就形成了所謂的兩步法。

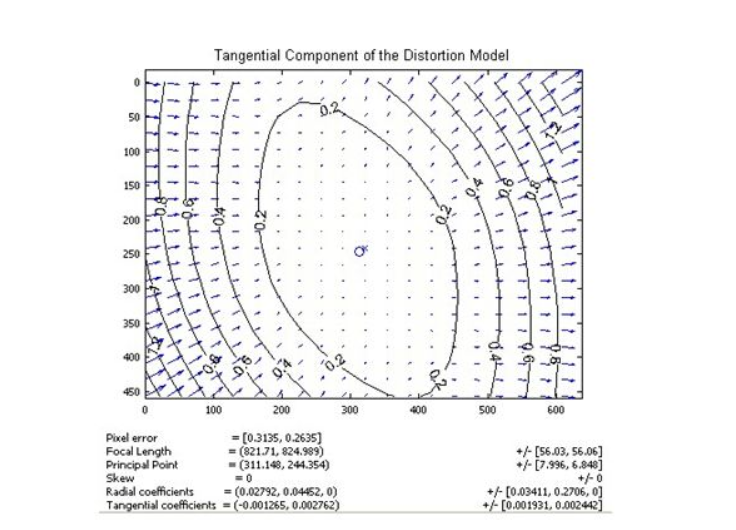
Tsai在他的論文中所使用的是典型的兩步法，但是在論文中僅考慮了攝像機的徑向畸變，而沒有考慮其切向畸變，在一些精確的測量系統中往往必須考慮切向畸變。根椐，Tsai的兩步標定法的攝像機模型，並結合攝像機的切向畸變，對攝像機的畸變模型進行了進一步的分析，並且在Matlab，中用兩步標定法得到精確標定的攝像機內外參數，並且通過可視化攝像機畸變模型，可以直觀了解畸變對圖像變形的影響。

攝像機模型

攝像機參數總是相對於某種幾何成像模型的，這個模型是對光學成像過程的簡化，比如最常用的針孔模型，它是攝像機標定研究的基本模型。其可以用簡單的數學公式表示物體和像面坐標之間的關係，然而很多情況下這種線性模型不能準確描述攝像機成像的幾何關係，如在近距、廣角時的情形，因此還需要考慮線性或非線性的畸變補償後，才能更合理地看作針孔模型成像過程。通常的針孔模型是一個隨著系統的扭曲像面坐標的校正量擴大的基準，常用的校正是由於透鏡的徑向畸變引起實際像點在圖像平面上徑向移動。如圖1所示，帶有徑向畸變的針孔模型能夠很好的反映成像關係。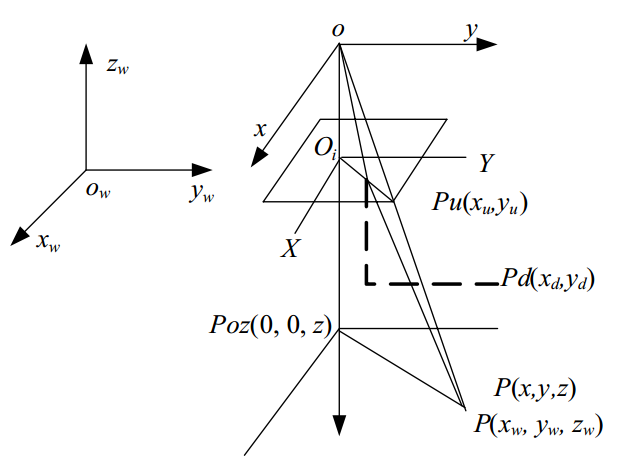

圖1 Tsai帶有徑向畸變的針孔模型

攝像機標定

傳統的標定方法起源於攝影測量學領域求解一個非線性的誤差函式的最小值問題。由於這種方法效率低並且運算量大，有人提出了增加限制條件的解決方法。直接線性變換法(DLT)通過直接求解線性方程來確定變換參數，這種算法簡捷，但未考慮透鏡的畸變，精度不高，結果的準確性對噪聲比較敏感，因此當要求高精度時它不是一種有效的方法，必須採用一種更加合適的攝像機模型。

非線性標定方法考慮了鏡頭畸變所引入的非線性方程，為求解數目眾多的未知數而採用了非線性最佳化方法。非線性最佳化求解未知參數，求解的結果常常取決於給定的初始值，如果初始值給定不合適，非線性搜尋最佳化計算容易陷入局部最小，很難得到正確的結果。綜合考慮上述兩種方法的優劣,如果先利用直接線性變換方法或者透視變換矩陣方法求解攝像機參數，再以求得的參數為初始值，考慮畸變因素，並利用最最佳化算法進一步提高定標精度的分步標定方法。

標定過程

Tsai在他的論文中首先提出了兩步法：①線性參數估計；②用非線性參數最佳化。研究根據兩步標定的方法，首先用DLT法直接線性估計攝像機的參數，再以得到的參數為初始值，進行非線性最佳化，得到參數的最優解。在Matlab中的運行結果顯示這種標定具有較高的精度，可以滿足大多數套用的需求。最後在Matlab中將攝像機畸變模型可視化，可以直觀的表示各畸變分量，其中畸變主要為徑向分量的影響，在大多數情況下其切向分量影響較小。

切向畸變的顯-隱式校正方法

矯正背景

圖像的畸變校正是計算機視覺領域中的關鍵技術之一。受鏡頭製造精度的影響，計算機視覺系統拍攝的圖像會出現不同程度的畸變，這種畸變可以分為徑向畸變和切向畸變兩種。對一般低精度要求的場合，只考慮徑向畸變就可以，因為切向畸變的影響遠小於徑向畸變。切向畸變的影響通常被忽略還有另一個原因，那就是含有切向畸變的校正模型是一個五次多項式，對這個多項式進行疊代求解是比較困難的。為此，提出了一種圖像畸變的顯-隱式校正方法，用顯-隱式校正模型代替傳統的五次多項式校正模型。此模型由徑向畸變係數(k1，k2)、切向畸變係數(p1，p2)和不含任何物理意義的隱式校正因子λn(1≤n≤4)共同構建，模型中隱式校正因子的求取用最小二乘法即可，之後用此模型進行圖像畸變的校正。

圖像畸變的形成

圖像畸變是指圖像平面上的圖像點在幾何位置上出現了誤差，從而使整個成像系統不再嚴格符合針孔成像模型。引起圖像畸變的誤差源主要有三種：徑向誤差、偏心誤差和薄稜鏡誤差。

圖2 徑向畸變和切向畸變

徑向誤差是由鏡頭表面部分在徑向曲率的變化存在缺陷造成的。它會直接導致圖像的徑向畸變。鏡頭部分的光學中心並不能嚴格的保持共線，相應地會產生偏心誤差。此外，由於鏡頭設計和生產以及攝像機組裝過程中的缺陷，還會引起薄稜鏡誤差。偏心誤差和薄稜鏡誤差在導致圖像的徑向畸變的同時，還會導致圖像的切向畸變。圖像的徑向畸變是指圖像點從它的理想位置向內或向外移動，即在徑向上出現誤差。而圖像的切向畸變是指圖像點在切向上出現偏移，如圖2所示。下面按照此三階段詳細介紹組合三角剖分法。

對圖像畸變的精確校正應該既對徑向畸變進行校正，又對切向畸變進行校正。最直接的思路就是通過攝像機標定求得徑向畸變係數(k1，k2)和切向畸變係數(p1，p2)，進而利用富含(k1，k2)、(p1，p2)的校正模型來校正圖像的畸變。由於這種校正模型中的(k1，k2)、(p1，p2)都是有真實物理意義的參數，故此這種校正方法稱為顯式校正。

研究結論

分析了圖像畸變的形成，為了同時校正圖像的徑向和切向畸變，提出了一種新的顯-隱式校正方法。此方法將顯式校正和隱式校正結合起來，彌補了二者的不足。實驗結果證明，顯-隱式校正方法可以有效地消除圖像的徑向和切向畸變，不但校正精度高，而且用最小二乘法即可求解。