分裂與賭法

分裂與賭法(splitting and roulette method )，是最有效的蒙特卡羅技巧之一，具有很強的普適性。

基本介紹

• 中文名：分裂與賭法
• 外文名：splitting and roulette method

分裂與賭法(splitting and roulette method )最有效的蒙特卡羅技巧之一由於它具有很強的普適性，因此，已被廣泛地編人許多著名的通用蒙特卡羅軟體中.分裂與賭方法的缺點是，需要使用者確定其中的若干參數，若確定得不好，反會出現事倍功半的現象.考慮如下二重積分的蒙特卡羅計算問題:

分裂與賭法

其中f(二，y)為隨機變數x與y的分布密度，g（二，）婦的二階矩存在.將x的積分區域分為兩部分:重要區域S和非重要區域k，則

同(xy)一樣，是上述二重積分的一個無偏統計量，其中M(x)表示以隨機變數x為自變數的整數函式;x與y服從分布`CxW sy二服從條件分布fx(y) (m = 1 2,'' .. M(二);叭·)為條件·的表征函式，當條件·成立時為1，否則為零;P(二)表示機率;子於[0,1]上均勻分布.分裂與賭法就是用上式作為蒙特卡羅估計的無偏統計量，式中前一部分與後一部分依次為分裂法部分與賭法部分.分裂與賭法常是成雙成對出現的，它的一般原理是:將其隨機變數的區域分為兩部分，原無偏統計量均方差大者為重要區域，小者為非重要區域，當該隨機變數屬於重要區域時，對其他隨機變數進行多抽樣，即進行分裂;屬於非重要區域時，對其他隨機變數是否抽樣進行一次賭，賭勝時抽樣，否則放棄抽樣.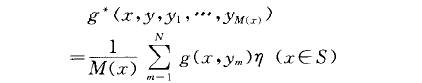

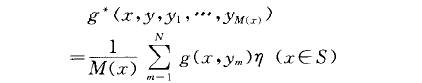
分裂與賭法

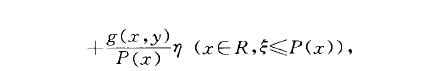
分裂與賭法