凱西定理

在數學中，凱西定理（Casey's theorem），也稱為廣義托勒密定理，是歐幾里德幾何中以愛爾蘭數學家 John Casey命名的定理。凱西定理及其反演可用於證明歐幾里德幾何中的各種陳述。

基本介紹

• 中文名：凱西定理
• 外文名：Casey's theorem
• 別名：廣義托勒密定理
• 相關人物：John Casey
• 套用：歐幾里得幾何證明

定理內容

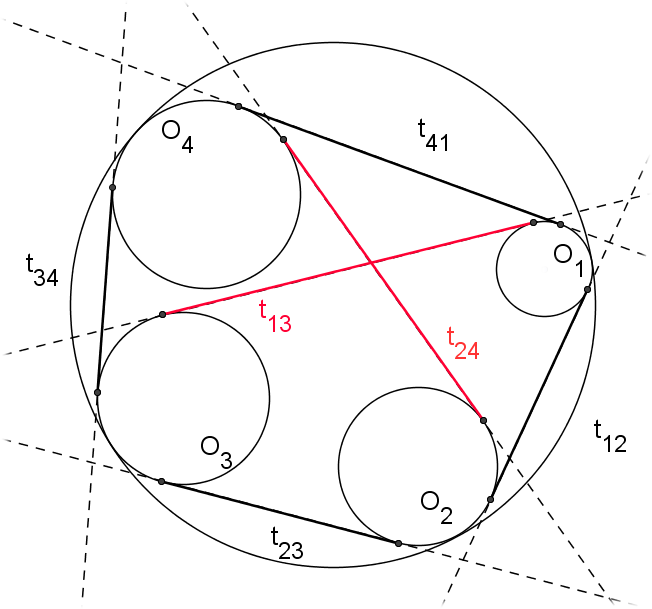
設 是一個半徑為 的圓， 是（按此順序）位於內部的四個不相交的圓圈， 和它相切， 表示圓 外部共同點的長度，然後：

請注意，所有四個圓都減少到點情況下，這正是托勒密定理。

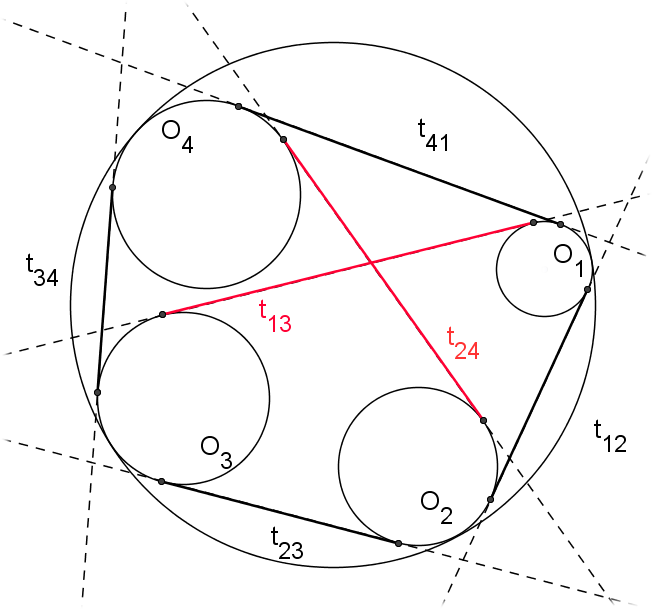
圖1.凱西定理

證明

半徑為 的圓 與圓 相切於點 ，用符號 表示圓的中心，畢達哥拉斯定理表示如下：

用點 來表示長度 。由三角形 的餘弦定律，

因為圓 相切：

設 成為圓 上的一個點，根據三角形 的正弦定律：

因此，

代入上述公式：

最後，求得長度

現在可以評估等式左側，藉助於原始托勒密定理套用於內切四邊形 :

進一步概括

可以看出，四個圓圈不必位於大圓圈內。事實上，它們也可能與外界相切。在這種情況下，應做出以下改變：

（1）如果都是從同一側切線（無論是在圓內還是在圓外）， 是外部公切線的長度；

（2）如果從不同的側面切線，是內部公切線的長度。

凱西定理的放過來也成立，即，如果等式成立，則圓圈與公共圓相切。