兩面角

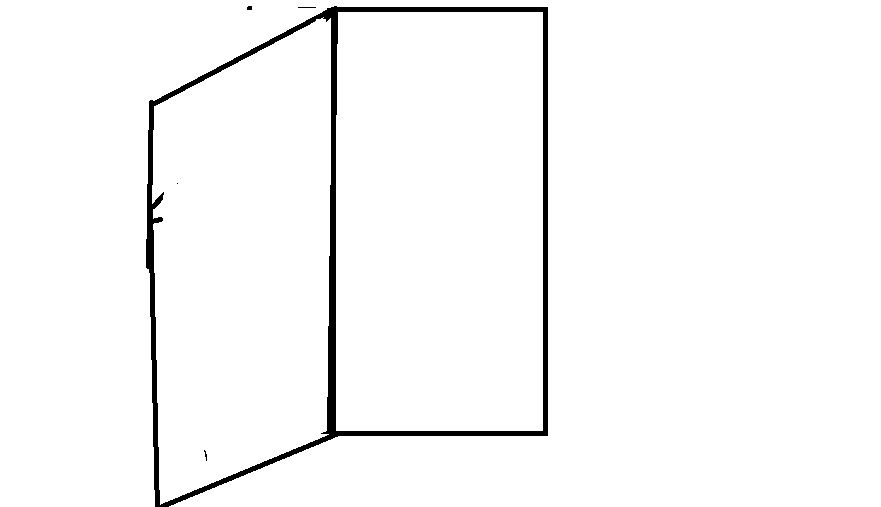
兩面角，又名二面角，是數學幾何中的算法：從一條直線出發的兩個半平面叫做二面角。

基本介紹

• 中文名：兩面角
• 外文名：Both sides Angle
• 適用範圍：空間平面
• 定義：從一條直線出發的兩個半平面
• 記法：二面角記為a-l-b
• 科目：數學

相關概念

半平面：一個平面里的一條直線，把平面分成兩部分，每一部分叫半平面。

棱：二面角的那條直線

面：其中的任意半平面。

記法

設兩面為a,b棱為l，則二面角記為a-l-b；

設兩面里各有一點A,B棱為CD，則二面角也可記為A-CD-B。

求法

一般求法

以二面角的棱上任意一點為端點，在兩個面里分別作垂直與棱的射線，這兩條射線所成的角叫做二面角的平面角。即：設兩面為a,b，棱為l,則所成的角y=∠AOB

其中A ∈a,AO⊥l,BO⊥l,O∈l,B∈b。

法向量法

設平面a,b的法向量為m,n且一個向上一個向下，則

a-l-b=<m,n>

cos(a-l-b)=cos<m,n>

cos(a-l-b)=|m*n|/|n||m|

平行向量法

有直線a,b分別平行於面γ,δ，且都垂直於棱l，設其方向向量為c,d，則二面角γ-l-δ等於

γ-l-δ=<c,d>

cos(γ-l-δ)=|c*d|/|c||d|

二面角的餘弦值

方程方法

設兩平面a,b方程分別為ax+by+cz+d=0和a1x+b1y+c1z+d1=0

則其二面角的餘弦值為(a*a1+b*b1+c*c1)/(a^2+b^2+c^2)^1/2(a1 ^2+b1 ^2+c1 ^2)^1/2。

兩平面垂直

定義

如果兩平面相交的二面角是直角，那么這兩個平面垂直。

符號表示：a∩b=l,m⊂a,m⊥l,n⊥l,n⊂b,n⊥m->a⊥b

判定定理

一個平面過另一個平面的垂線，則這兩個平面垂直。

符號表示： l⊂a,l⊥b-->a⊥b

證明：設a∩b=m,l∩m=O

∵l⊥b,m⊂b

∴l⊥m

在b里過O作n⊥m.

∵l⊥b,n⊂b

∴l⊥n

又n⊥m，

∴a⊥b

垂直於同一平面的相交平面垂直。

符號表示：a⊥y,b⊥y,a∩b=l-->a⊥b

證明：設y∩b=m,a∩y=n

根據定義得l⊥m,l⊥n

又a∩b=l,m⊂a,n⊂b

∴a⊥b

性質

兩個平面垂直，則一個平面內垂直於交線的直線與另一個平面垂直。

符號表示：a⊥b,a∩b=l,m⊥l,m⊂a-->m⊥b

證明：設l∩m=O

在b內，過過O作n⊥m：

根據兩平面垂直的定義得n⊥l。

∵n⊂b,m⊂b,n⊥l

∴n∩l=M.

∵n⊂b,l⊂b,n∩l=M,m⊥l,n⊥m

∴m⊥b

兩個相交平面都垂直於第三個平面，則它們的交線垂直於第三個平面。

符號表示：a⊥y,b⊥y,a∩b=l-->l⊥y

證明：設a∩y=n,b∩y=m

根據定理得a⊥b,

根據定義得l⊥n,l⊥m,n⊥m，

∵n⊂y,m⊂y,n⊥l

∴n∩l=M.

∵n⊂y,m⊂y,n∩l=M,m⊥l,n⊥l

∴l⊥y