偽球線匯(pseudo-spherical congruence)一種重要而特殊的線匯。
基本介紹
- 中文名:偽球線匯
- 外文名:pseudo-spherical congruence
設線匯的兩個焦曲面(假設存在,例如在雙曲型線匯情形)分別記為M,M",線匯是M,M‘的公共切線族.p: M--M‘是自然映射,它使M上的焦點二映成M‘上的對應焦點x" _p(x).稱這樣的線匯為偽球線匯,如果它滿足:
1. x一二‘=r,r=const.
2.對應點x,x‘處M,M‘的單位法向量e3 , ea交成定角:,亦即。。 e3 -cosr,r=const.
偽球線匯的兩個焦曲面M,M‘具有相等的負常數高斯曲率
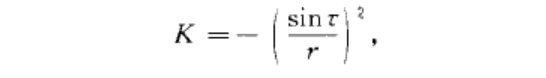
偽球線匯
這一結果通常稱之為白克龍定理.由上述結果,若線匯的一個焦曲面具有常負高斯曲率K=-1,則另一個焦曲面亦然.於是,它們分別為SG (Sine-Gor-don)方程的解.因此,從SG方程的已知解構造新解的問題歸結為如何從常負曲率曲面M構造一個偽球線匯的問題.這就是白克龍變換的幾何表述.
