信元丟失比

信元丟失比(CellLossRatio)是在ATM信元標題的一個域，其指出丟失信元的和成功傳輸的信元的比率。當連線建立時，CLR能夠被設定成一個服務質量（QoS）參數。

信元丟失率分析是研究ATM網路中流量控制問題的基礎和關鍵。在ATM網路設計中,須限制信元丟失率以滿足各業務的服務質量要求:過高的信元丟失會降低話音和多媒體視頻等在目的終端的重現效果。

中文名稱	信元丟失比
英文名稱	cell loss ratio;CLR
定　　義	在異步轉移模式(ATM)網路中，表示丟失的信元數與全部傳送信元數之比的性能參數。
套用學科	通信科技（一級學科），交換選路（二級學科）

基本介紹

• 中文名：信元丟失比
• 外文名：cell loss ratio
• 別名：信元丟失率
• 套用學科：通信科技，交換選路
• 領域：ATM網路
• 簡稱：CLR

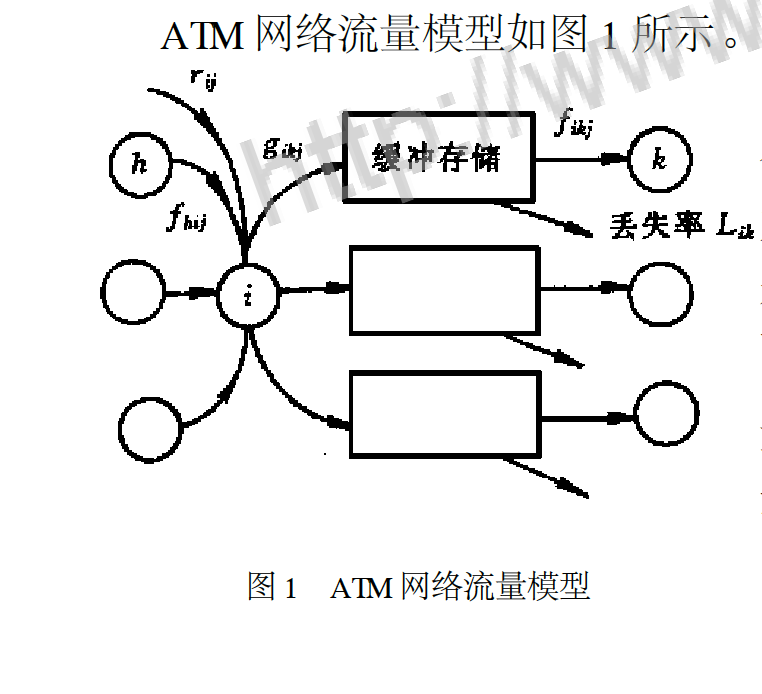
信元丟失問題

CLR分析

基於ATM技術的寬頻綜合業務數字網可以承載各種各樣的通信業務,信元丟失率分析是研究ATM網路中流量控制問題的基礎和關鍵。在ATM網路設計中,須限制信元丟失率以滿足各業務的服務質量要求:過高的信元丟失會降低話音和多媒體視頻等在目的終端的重現效果。

丟失原因

ATM網路中信元丟失原因大致有:交換節點存儲信元佇列的快取區不夠,路由選擇不當,傳輸過程中出現差錯,擁塞控制不力等。

三種信元丟失類型即交換結構中的丟失、快取區溢出造成的丟失及擁塞控制中信元的丟失

交換節點信元丟失和交換結構有關,以輸出快取Knockout交換結構為例。若每一輸出快取器狀態用每一時隙內信元數表示,其狀態轉移過程可用Markov鏈描述,信元丟失率在給定的網路結構中隨著流量Gik 增大而增大, 而且輸出快取區B的大小對信元丟失率影響很大。

ON-OFF模型

在該模型中,每一業務源或都處於active狀態(產生數據),或處於idle狀態(無數據產生),且2個狀態交替出現形成周期特徵。為了建立我們需要的多業務源,單佇列系統模型,我們先建立單一業務源模型,然後建立多業務源,並在多業務源的基礎上建立起需要的多業務源—單佇列系統模型。

在多業務源組模型中,各業務源可能同時產生數據,即信元產生突發事件並發進行,也可能在相互獨立的時間點上進行。因此我們將其分為悲觀情況、樂觀情況以及處於悲觀和樂觀之間的情況的三種狀態。

悲觀情況

悲觀情況下,為避免信元丟失,網路設計時,佇列容量X和輸出鏈路容量C就須滿足,既要保證每周期的激活狀態時間ton內,系統能容納所產生的所有信元,又要保證在一個周期(T)內輸出鏈路能傳遞所有本周期產生的信元。

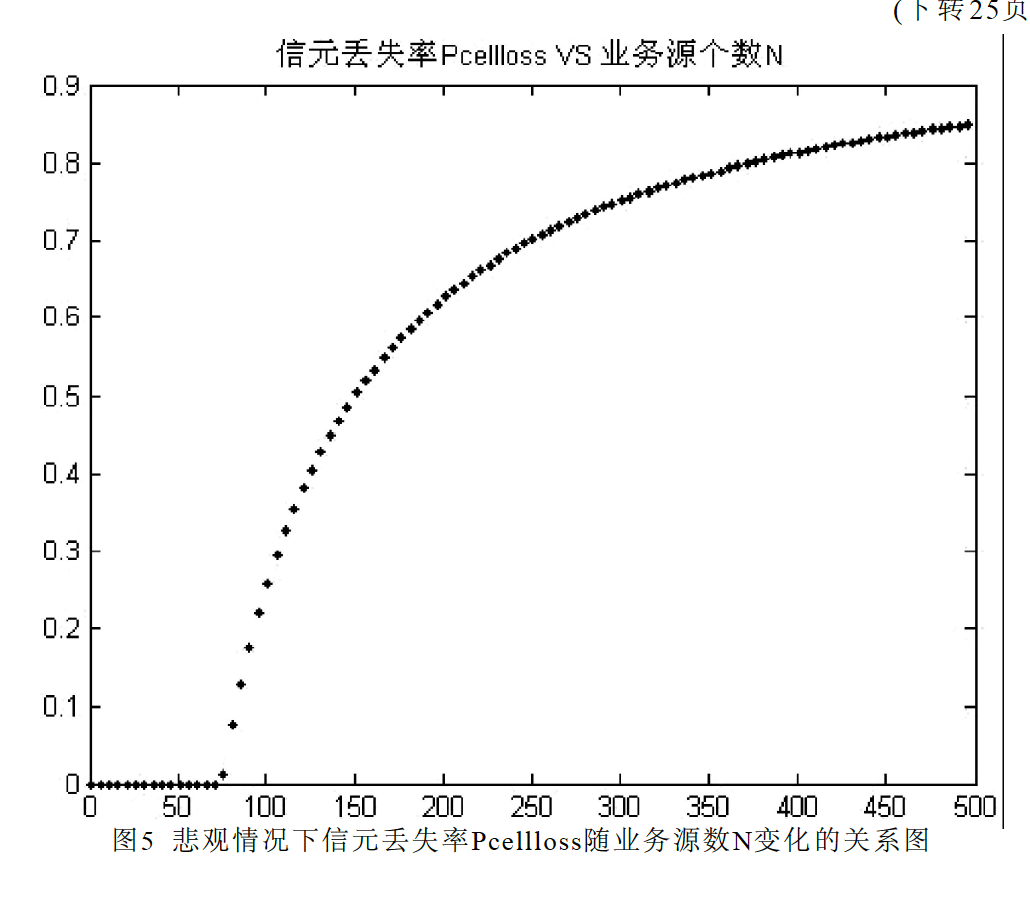
悲觀情況下信元丟失率Pcellloss隨業務源數N變化的關係圖

如《悲觀情況下信元丟失率Pcellloss隨業務源數N變化的關係圖》所示可以看出業務源數N小於某一臨界值時,理論丟包率為零,當超過這一臨界值時信元丟失的穩態機率Pcellloss隨業務源數N的增加而變大。

樂觀情況

信源組的每一個信源的數據產生開始時間均勻地分布在每個信息周期[0,T]內。

假設業務源數目為N,且有相同的特性參數:t-on, t-off及R(每秒產生的信元數),輸出鏈路容量為C(佇列在非空閒時,每秒以C個信元的速率減少),佇列容量為X。

在樂觀情況下,根據ton的長度特徵分為2種情況:①一個信源激活期的結束時刻正好有另一個源激活期的開始,即滿足 ,即激活時間ton為(T/N)的整數倍,在這種情況下信源組的信元到達速率固定為mR,如圖2所示

ton為T/N的整數倍;(當信元的激活時間t on不為(T/N)的整數倍時,即mT/N

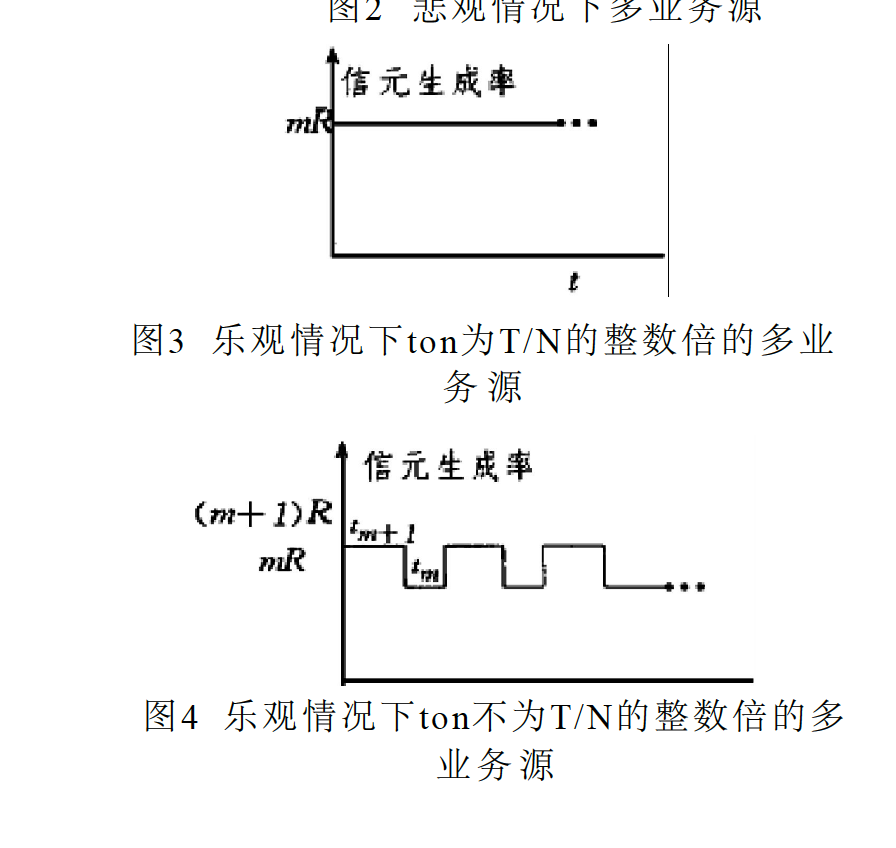
圖2

CLR估計

信元丟失率的估計可以分為兩個步驟: 首先考慮更新時刻點緩衝區佇列情況, 由於更新過程的無關性, 其佇列情況可以用嵌入式馬爾柯夫鏈來表示, 求出更新點隊長分布的極限機率;然後套用報酬更新定理得出緩衝區的信元丟失率。

1) 更新時刻點的隊長分布極限機率

2) 信元丟失率

信元丟失率等於丟失信元數除以到達信元數 , 根據報酬更新定理 , 有

信元丟失率clp = 一個更新周期內的平均丟失信元數

一個更新周期內的平均到達信元數

目前的佇列研究中使用的分析模型都是基於低階統計特性的, 如研究最成熟套用最廣泛的佇列分析方法On-Off源疊加模型法, 包括MMPP和MMDP等。這類分析方法將輸入通信量擬合成多個簡單On-Off 源的疊加, 然後運用排隊論估計緩衝區的信元丟失率, 最後的分析結果通常用馬爾柯夫極限機率來表示。但是在一些套用場合(如VBR 視頻源) , 已知的是輸入通信量的頻寬分布和自相關特性, 套用上述方法存在著模型擬合的困難, 例如在擬合頻寬分布時, 需根據馬爾柯夫鏈的極限分布逆推轉移矩陣, 這往往是很困難的。於是產生了這樣一個問題: 如何直接根據已知輸入通信量的頻寬分布和自相關特性來估計緩衝區的信元丟失率。

解決這個問題的關鍵是設計一個模型, 既要能提供對通信量低階統計特性的直接擬合, 又要具有良好的理論可分析性。目前為止還沒有研究報導同時滿足上述兩個條件的模型, 如其中擬合能力最強的TES 模型雖然滿足第一個條件卻無法進行理論分析。