伯格算法（burg algorithm)一種直接由已知的時間信號序列計算功率譜估計值的遞推算法。由於是J．P·伯格提出的，故得名伯格算法。
基本介紹
- 中文名：伯格算法
- 外文名：burg algorithm
- 套用學科：通信
定義,改進,
定義
伯格遞推算法可以表達如下：
令X（L)，x（L+l)，…，x(U)為已知時間信號序列，則利用此序列即可進行以下的遞推算法，即設初始值
並利用遞推公式：
另外：
根據伯格遞推算法直接由時間信號序列計算預測誤差濾波器參數或及AR模型型參數，由下式
求出最大熵法功率譜估值。式中M是預測濾波器階數，PM是M階預測濾波器誤差輸出功率；△t是抽樣周期；am=Km是預測濾波器的參數。
伯格遞推算法只需要知道有限長的時間信號序列，不需計算其自相關函式值，所得的解保證是穩定的。該算法對於較短的數據序列的功率譜估計很有效。因此伯格算法在許多領域得到套用。
套用伯格遞推算法往往使譜估值出現“譜線分裂”與“頻率偏移”等問題，因而，又有各種改進的算法。其中，較著名的有傅格算法和馬普爾算法，但是所需的計算量較大。
改進
高分辨譜估計的伯格算法自問世以來,因其計算量較小而得到了廣泛的套用。 然而 ,大量計算表明 ,當數據為實數樣本時 ,譜估計的性能不盡人意。特別是在某些數據長度 T下 ,頻率估計偏差受信號初相位的影響較大 ,有時可達到 1/( 16T )的量級。 因此尋求改進算法以減小頻率估計偏差仍是近年來研究的課題。 採用加權伯格算法可部分改善譜估計的性能。已經有人對伯格算法產生譜估計偏差的原因進行過各種分析和猜測。分析其中一種產生譜偏差的原因 ,並在此基礎上提出一種改進算法。 文中推導了這種改進算法 ,並給出了計算步驟。 計算機仿真結果表明 ,與伯格算法相比 ,改進算法的譜估計偏差明顯減小。
在實數據情況下 ,由伯格算法得到的譜有時會出現譜分裂和譜峰偏移。 已有文獻對這種現象產生的原因作了各種分析和猜測。 其中之一認為由於一階反射係數的計算存在誤差 ,導致預測誤差濾波器 ( PEF )其餘係數計算的誤差。 根據這種分析 ,本文提出了一種改進算法。 該算法不是直接利用伯格算法計算一階反射係數 ,而是按二階 PEF輸出總功率最小的原則 ,求解二階 PEF係數 ,再求得一階反射係數。 在獲得二階 PEF係數之後 ,仍用伯格遞推算法求其他高階係數。 結果 ,在幾乎不增加計算量的情況下 ,使譜估計的性能得到明顯改善。 對信號長度為 1/4信號周期的奇數倍且初相為 π /4時的最壞情況 ,在計算機上進行了計算。結果表明 ,譜峰偏移大為減小。
伯格算法在計算一階反射係數時引入了誤差 ,因而利用遞推公式計算各階反射係數和 PEF係數時均造成誤差。 結果 ,使譜估計的峰值產生偏差 ,特別是當信號長度為 1/4信號周期的奇數倍且初相為 π /4(或其奇數倍 )時最為嚴重。改進算法不直接計算一階反射係數 ,而是通過 2階 PEF係數再求一階反射係數 ,結果使得到的一階反射係數與初相無關 ,從而使譜峰偏差減小 ,改善了譜估計的質量。由式 ( 12 ～ 15)不難得知 ,改進算法實際上並不增加運算量。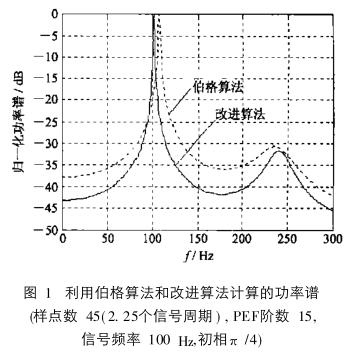
圖 1 利用伯格算法和改進算法計算的功率譜
圖 1 利用伯格算法和改進算法計算的功率譜圖 1為利用伯格算法和改進算法計算的功率譜（樣點數45（2.25個信號周期），PEF階數15，信號頻率100Hz，初相PI/4）
