表達式,適用條件,推導,牛頓第二定律推導,能量守恆定律推導,伯努利,一次衝撞事件,套用舉例,球類比賽中的“旋轉球”,列車(捷運)站台的安全線,船吸現象,颳風掀翻屋頂,噴霧器,離心式水泵,文丘里流量計,
表達式
即伯努利方程。其中,
為流體中某點的壓強,
為流體在該點的流速,
為流體密度,
為重力加速度,
為該點所在高度,
是一個常量。它也可以被表述為:
適用條件
伯努利原理並非適用於全部流體,而是只適用於描述理想流體的運動。因此要求流體滿足:
具有連續性:理想流體在任何給定的流動狀態下都能保持連續性,即在任何給定的時刻和位置,流體的質量和體積都是連續分布的。
不可壓縮性:理想流體在流動過程中保持體積不變,即體積幾乎沒有變化。
無黏性:理想流體沒有黏性或稱為無黏性,即在理想流體中,分子之間沒有內部摩擦力,流體在外力作用下可以自由地流動。
流體沿流線運動,流線彼此不相交。
推導
伯努利方程可以分別由牛頓第二定律以及能量守恆定律推導得來。
牛頓第二定律推導
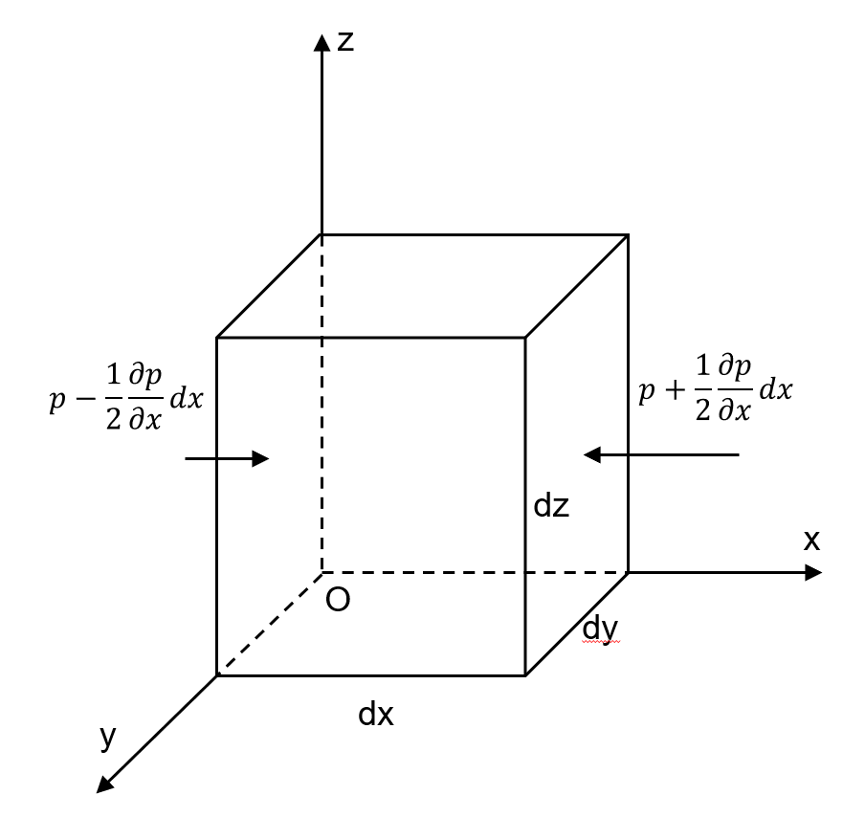
如圖,取液體中的一微體,對於x方向,作用在微體上的力有兩個方向的壓力
、
以及體積力
,X為體積力項係數,由牛頓第二定律可得
同理可得
將上面三式相加化簡可得
對於理想流體,為常數,在重力場中X=Y=0,Z=-g,於是可將上式化簡,得
即
能量守恆定律推導
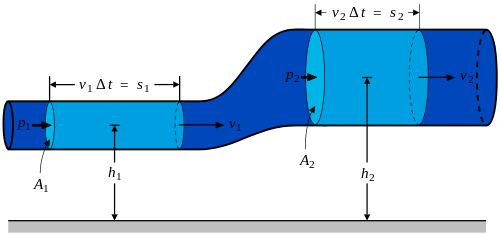
如圖所示,假設理想流體在一個管道中中流動。設 W 表示在面積 A 上施加壓力 p 所做的功,為引發的體積變化量,在1、2兩個點的壓力做功分別為
兩點壓力做功之差為
同時,由能量守恆定律可知,壓力做功之差應等於動能和勢能差之和
由上述兩式可得
整理,得
圖文解釋:
丹尼爾·伯努利在1726年首先提出時的內容就是:在水流或氣流里,如果速度小,壓強就大,如果速度大,壓強就小。這個原理當然有一定的限制,但是在這裡我們不談它。別萊利曼的書里有幾個通俗易懂的例子:
在圖1中,向AB管吹進空氣。如果管的切面小(像a處),空氣的速度就大;而在切面大的地方(像b處),空氣的速度就小。在速度大的地方壓力小,速度小的地方壓力大。因為a處的空氣壓力小,所以C管里的液體就上升;同時b處的比較大的空氣壓力使D管里的液體下降。
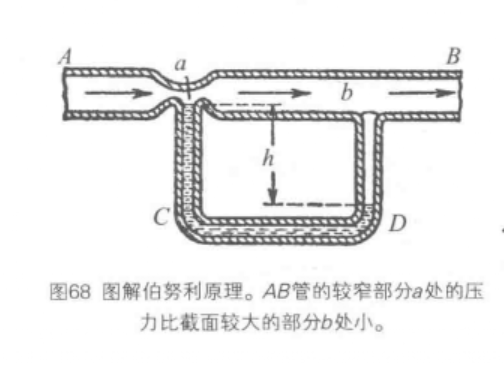
圖1 圖解伯努利原理
在圖2中,T管固定在鐵制的圓盤DD上,下面還有一個跟T管不相連的圓盤dd。空氣從T管里出來以後,還要從兩個圓盤之間間隙流出去,剛從T管里出來的空氣流速很大,但是越接近盤邊,空氣的流速就越小,因為氣流從兩盤之間流出來,切面在迅速加大,但是圓盤四周的空氣壓力是很大的,因為這裡的氣流速度小;而圓盤之間的空氣壓力卻很小,因為這裡的氣流速度大。因此圖盤周圍的空氣對圓盤的壓力較大,
周圍空氣的壓力試圖把兩個圓盤推到一起;結果是,從T管里吹出的氣流越強,圓盤dd被吸向圓盤DD的力也越大。
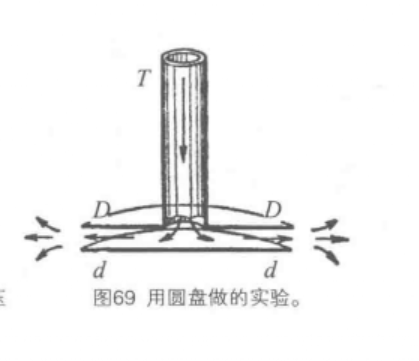
圖2 用圓盤做的實驗
圖3和圖2相似,所不同的只是用了水。如果圓盤DD的邊緣是向上彎曲的,那么在圓盤DD上迅速流動著的水會從原來比較低的水面自己上升到跟水槽里的靜水面一般高。因此圓盤下面的靜水就比圓盤上面的動水有更高的壓強,結果就使圓盤上升。軸P的用途是不讓圓盤向旁邊移動。
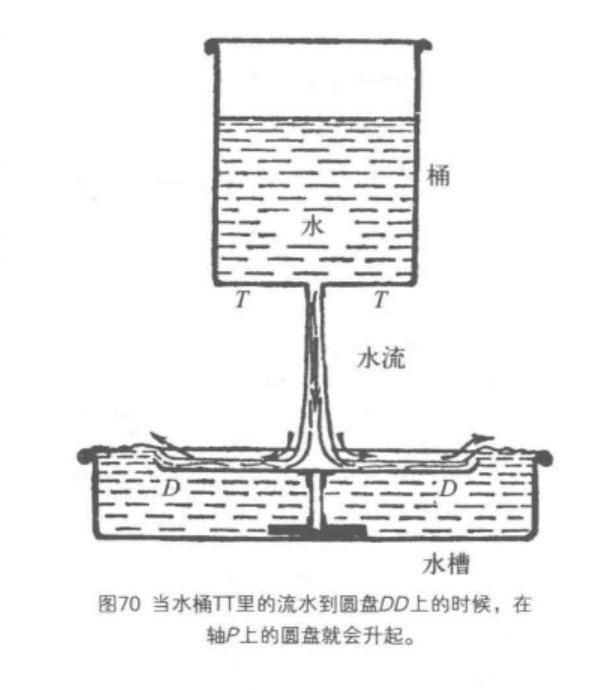
圖3
圖4畫的是一個飄浮在氣流里的很輕的小球。氣流衝擊著小球,不讓它落下來。當小球一跳出氣流,周圍的空氣就會把它推回到氣流里,因為周圍的空氣速度小,壓力大,而氣流里的空氣速度大,壓力小。
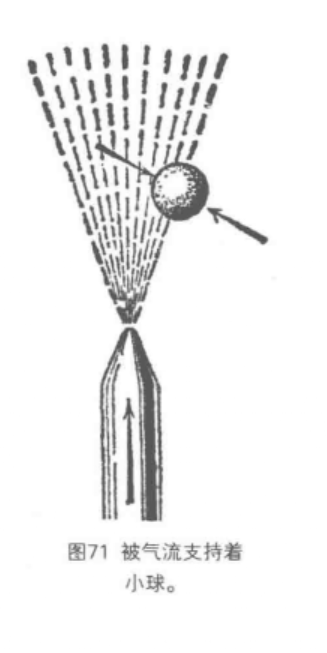
圖4 被氣流支持著的小球
圖5(a)中的兩艘船在靜水裡並排航行著,或者是並排地停在流動著的水裡。兩艘船之間的水面比較窄,所以這裡的水的流速就比兩船外側的水的流速高,壓力比兩船外側的小。結果這兩艘船就會被圍著船的壓力比較高的水擠在一起。海員們都知道,兩艘並排駛著的船會互相強烈地吸引。
如果兩艘船並排前進,而其中一艘稍微落後,像圖5(b)所畫的那樣,那情況就會更加嚴重。使兩艘船接近的兩個力,會使船身轉向,並且船B轉向船A的力更大。在這種情況下,撞船是免不了的,因為舵已經來不及改變船的方向。
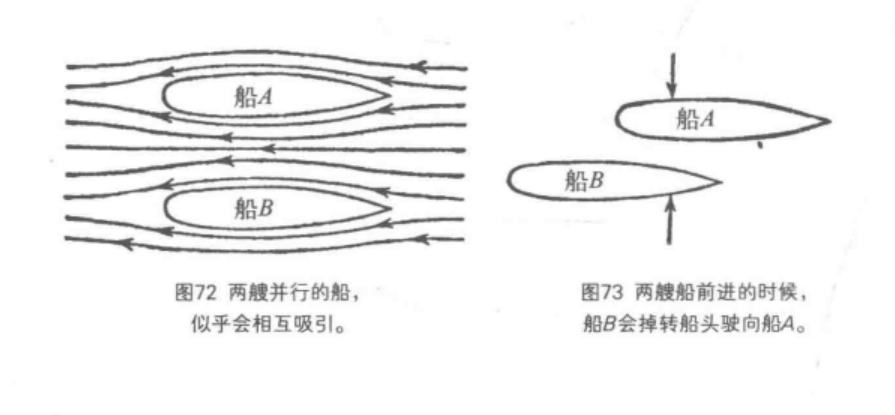
圖5
圖5 兩艘船並行。(a)兩艘並行的船會相互吸引;(b)兩船並行,一船稍微落後。
在圖5中所說的這種現象,可以用下面的實驗來說明。把兩個很輕的橡皮球照圖6那樣吊著。如果你向兩球中間吹氣,它們就會彼此接近,並且互相碰撞。

圖6 如果向兩個氣球之間吹氣,它們會彼此接近,然後相撞
伯努利
丹尼爾·伯努利[1] (1700年-1782年)出生於荷蘭的格羅寧根,16歲時獲藝術碩士學位,21歲時又獲得醫學博士學位。他曾申請解剖學和植物學教授職位,但未成功。
丹尼爾受父兄影響,一直很喜歡數學。1724年,他在去威尼斯的旅途中發表了《數學練習》一文,引起學術界關注,並被邀請到聖彼得堡科學院工作。1725年,25歲的丹尼爾受聘為聖彼得堡科學院生理學院士和數學院士。1727年,20歲的歐拉(後人將他與阿基米德、牛頓和高斯並列為數學史上的“四傑”)到聖彼得堡工作,成為丹尼爾的助手。
然而,丹尼爾不習慣聖彼得堡的生活,在8年以後的1733年,他找到機會返回巴塞爾,終於在那兒成為解剖學和植物學教授,後又成為物理學教授。
1734年,丹尼爾榮獲巴黎科學院獎金,以後又10次獲得該獎金。能與丹尼爾媲美的只有大數學家歐拉。丹尼爾和歐拉保持了近40年的學術通信,在科學史上留下了一段佳話。
在伯努利家族中,丹尼爾是涉及科學領域較多的人。他出版了經典著作《流體動力學》,研究了彈性弦的橫向振動問題,提出了聲音在空氣中的傳播規律。他的論著還涉及天文學、地球引力、潮汐、磁學、振動理論、船體航行的穩定和生理學內容等。博學的丹尼爾成為伯努利家族的代表人物。
丹尼爾於1747年當選為柏林科學院院士,1748年當選巴黎科學院院士,1750年當選英國皇家學會會員。
1782年3月17日,丹尼爾·伯努利在瑞士巴塞爾逝世,終年82歲。
一次衝撞事件
1912年的秋天,當時世界上最大的輪船之一、遠洋貨輪“奧林匹克號”正在大海上航行。突然,一艘比它小得多的鐵甲巡洋艦“豪克號”從後面追了上來,在離它100m的地方幾乎跟它平行地疾馳。就在這時,一件意外的事情發生了:“豪克號”好像著了魔似的,竟然扭轉船頭朝“奧林匹克號”沖了過來,“豪克號”上的舵手怎么操作也沒有用。結果,“奧林匹克號”無可奈何地接受了“豪克號”的親密接觸,並付出了極大的代價——船舷被“豪克號”撞了一個大洞。
在海事法庭審理這件奇案的時候,“奧林匹克號”的船長被判為有過失的一方,法院認為,這是因為他沒有發出任何命令給橫著撞過來的“豪克號”讓路。船長雖然感到自己很冤枉,但沒有辦法解釋,只好蒙冤受屈。案子就這樣結束了,但這件事情卻引起了一些科學家的注意,他們認為這次事件一定事出有因。
其實,早在1726年,丹尼爾·伯努利(1700-1782)就已經注意到:如果水沿著一條有寬有窄的溝(或粗細不均的管子)向前流動,溝的較窄部分就流得快些,但水流對溝壁的壓力比較小;反之,在較寬的部分水就流得較慢,壓向溝壁的力則會比較大。這一發現,後來被人們稱為伯努利原理。
這個原理雖然發現得較早,但一直不被人們重視。出現了“奧林匹克號”被撞事件後,一些科學家突然想到,用這一原理來解釋這次事故是非常合情合理的。於是,自此以後伯努利原理才漸漸得到了它應受的重視。這是一條普遍性的原理,它不僅對於流動的水是適用的,而且對於流動的其他液體甚至氣體也適用。
套用舉例
球類比賽中的“旋轉球”
球類比賽中的“旋轉球”具有很大的威力。旋轉球和不轉球的飛行軌跡不同,是因為球的周圍空氣流動情況不同造成的。不轉球水平向左運動時周同空氣的流線。球的上方和下方流線對稱,流速相同,上下不產生壓強差。再考慮球的旋轉,轉動軸通過球心且平行於地面,球逆時針旋轉。球旋轉時會帶動周同得空氣跟著它一起旋轉,致使球的下方空氣的流速增大,上方的流速減小,球下方的流速大,壓強小,上方的流速小,壓強大。跟不轉球相比,旋轉球因為旋轉而受到向下的力,飛行軌跡要向下彎曲。
列車(捷運)站台的安全線
在列車(捷運)站台上都劃有黃色安全線。這是因為列車高速駛來時,靠近列車車廂的空氣被帶動而快速運動起來,壓強就減小,站台上的旅客若離列車過近,旅客身體前後會出現明顯的壓強差,身體後面較大的壓力將把旅客推向列車而受到傷害。所以在火車(或者是大貨車、大巴士)飛速而來時,旅客應站在安全線外規範等待。
船吸現象
當兩艘船平行著向前航行時,在兩艘船中間的水比外側的水流得快,中間水對兩船內側的壓強,也就比外側對兩船外側的壓強要小。於是,在外側水的壓力作用下,兩船漸漸靠近,最後相撞。現在航海上把這種現象稱為“船吸現象”。
颳風掀翻屋頂
當颳風時,屋頂上的空氣流動得很快,而屋頂下的空氣幾乎是不流動的。根據伯努利原理,這時屋頂下氣壓大於屋頂上的氣壓。風速越快,屋頂上下的壓力差越大,一旦風速超過一定程度,這個壓力差就會導致屋頂被掀飛。
噴霧器
噴霧器是利用流速大、壓強小的原理製成的。讓空氣從小孔迅速流出,小孔附近的壓強小,容器里液面上的空氣壓強大,液體就沿小孔下邊的細管升上來,從細管的上口流出後,液體受到空氣流的衝擊,被噴成霧狀。
汽油發動機的化油器的原理與噴霧器原理相同。
離心式水泵
泵殼匯集從各葉片間被拋出的液體,這些液體在泵殼內順著蝸殼形通道逐漸擴大的方向流動,流速逐漸減小,壓力逐漸增大,流體的動能轉化為靜壓能,減小能量損失。所以泵殼的作用不僅在於匯集液體,它更是一個能量轉換裝置。
文丘里流量計
文丘里流量計是測量流體壓差的一種裝置。它是一個先收縮而後逐漸擴大的管道。在收縮段的直管段截面1和截面2兩處,測量靜壓差和兩個截面的面積,並用伯努利方程即可計算出通過管道的流量。需要注意的是,由於收縮段的能量損失要比擴張段小得多,所以不能用擴張段的壓強來計算流量,以免增大誤差。