二階線性系統

二階線性系統簡稱“二階系統”。包含有兩個獨立的狀態變數的動態系統。可分為二階線性負反饋系統和二階線性正反饋系統。二階線性負反饋系統的行為特徵是尋找目標。一般分為欠阻尼形式和過阻尼形式。欠阻尼行為模式下，系統變數先是超過了終值，但最後則從衝過的峰值開始下降，呈減幅振盪，最終趨於目標值。這種行為可能是由於反饋迴路中過長的延遲造成，也可能是由於校正系統與系統目標之間的偏差作用過於強烈而造成。過阻尼行為模式是單調地趨於目標值。二階線性正反饋系統的行為特徵為趨於無窮，但呈兩種不同的模式，一種是單調地趨於無窮，另一種是系統行為作增幅振盪。二階線性系統與一階系統相比，最大的不同是它可能產生振盪行為，包括等幅振盪、減幅振盪和增幅振盪三種形式。

基本介紹

• 中文名：二階線性系統
• 外文名：second-order linear system
• 簡稱：二階系統
• 含義：指凡用二階微分方程描述的系統
• 包含：兩個獨立的狀態變數的動態系統
• 涉及學科：信息科學

類型

二階線性系統（second-order linear system）簡稱“二階系統”。指凡用二階微分方程描述的系統。許多高階系統在一定的條件下，常常近似地作為二階系統來研究。包含有兩個獨立的狀態變數的動態系統。可分為二階線性負反饋系統和二階線性正反饋系統。

二階線性負反饋系統

二階線性負反饋系統的行為特徵是尋找目標。一般分為欠阻尼形式(如圖a)和過阻尼形式(如圖 b)。

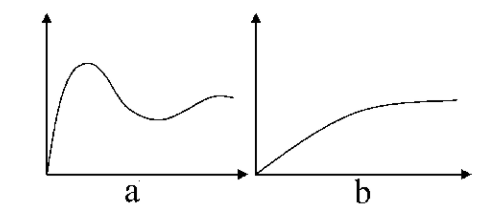
欠阻尼行為模式下，系統變數先是超過了終值，但最後則從衝過的峰值開始下降，呈減幅振盪，最終趨於 目標值。這種行為可能是由於反饋迴路中過長的延遲造成，也可能是由於校正系統與系統目標之間的偏差作 用過於強烈而說獄台造成。過阻尼行為模式是單調地趨於目 標值。

二階線性正反饋系統

二階線性正反饋系統的行為特徵為趨於無窮，但呈兩種不同的模式，一種是單調地趨於無窮(如圖c)，另 一種是系統行為作增幅振榜拜跨盪(如圖d)。

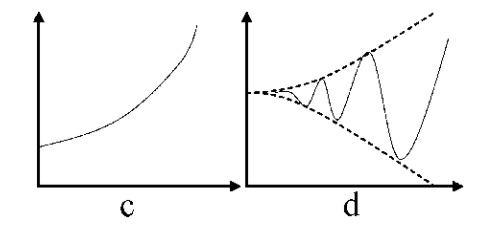
二階線性系統與 一階系統相比，最大的不同是它可能產生振盪行為，包括等幅振盪、減幅振盪和增幅振盪三種形式。

數學模型分類

二階系統控制系統按數學模型分類時的一種形式是，用數學模型可表示為二階線性常微分方程的系統。二階系統的解的形式，可由對應傳遞函式W(s)的分母多項式P(s)來判別和劃分。P(s)的一般形式為變換運算元s的二次三項代數式，經標準化後可記為代數方程P(s)=0的根,可能出現四種情況:

1.兩個實根的情況,對應於兩個串聯的一階系統.如果兩個根都是負值,就為非周期性收斂的穩定情況.

2.當a1=0,a2>0,即一對共軛虛根的情況,將引起頻率固定的等幅振盪,是系統不穩定的一種表現.

3.當a1<0,a1-4a2<0,即共軛復根有正實部的情況,對應於系統中發生髮散型的振盪,也是不穩定的一種表現.

4.當a1>0,a1-4a2<0,即共軛復根有負實部的情況,對應於收斂型雅煉鍵汽振盪,且實部和虛部的數值比例對輸出過程有很大的影響.一般以阻尼係數ζ來表征,常取

在0.4~0.8之間為宜.當ζ>0.8後，振盪的作用就不顯著,輸出的速度也比較慢.而ζ<0.4時，輸出量就帶有明顯的振盪和較大的超調量，衰減也較慢，這也是控制系統中所不希放殼束望的。

相軌跡

許多本質性非線性系統常常可以進行分段線性化處理，而許多非本質性非線性系統也可以在平衡點附近做增量線性化處理。因此，可以從二階線性系統的相軌跡入手進行研究，為非線性系統的相平面分析提供手段，

由描述的二階線性系統自由運動的微分方程

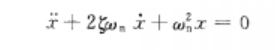
可得拘烏

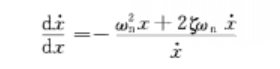
根據式利用等傾斜線才主罪法，或者從式解出系統的相軌跡方程，就可以繪製出相應的相平面圖。將不同情形下的二階線性系統相平面圖歸納整理，列在下圖中。

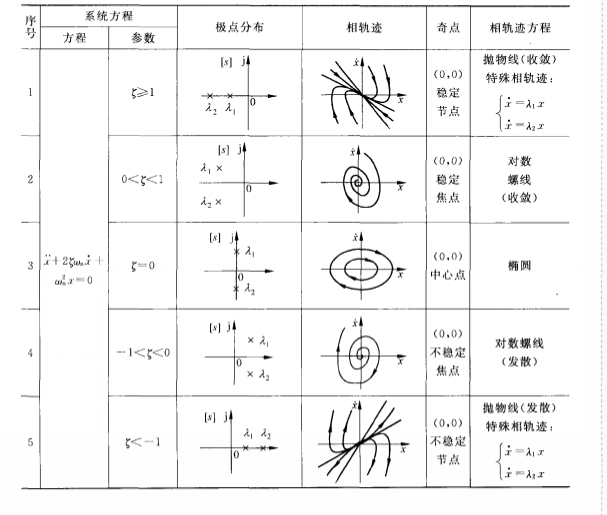二階線性系統的相軌跡

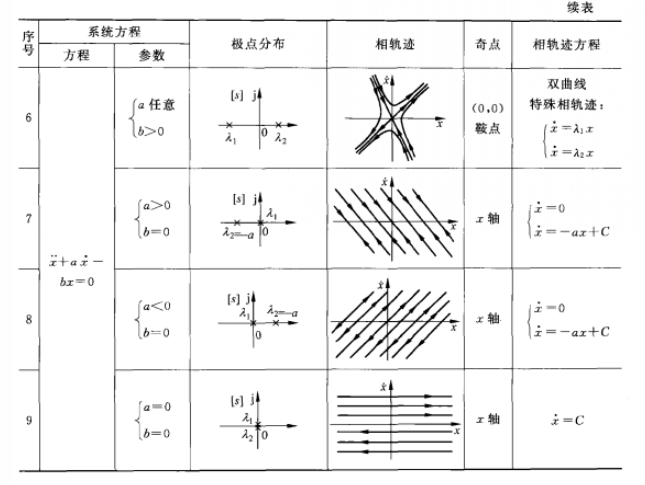二階線性系統的相軌跡續表

在式中令x"=x'=0可以得出唯一解x_e=0，這表明線性二階系統的奇點〔或平衡點)就是相平面的原點。根據系統極點在複平面上的位置分布，以及相軌跡的形狀，將奇點分為不同的類型。

①當ξ>=1時，λ₁，λ₂為兩個負實根，系統處於過阻尼(或臨界阻尼)狀態，自由回響按指數衰減。對應的相軌跡是一簇趨向相平面原點的拋物線，相應奇點稱為穩定的節點。

②當0<ξ<1時，λ₁，λ₂為一對具有負實部的共扼復根，系統處於欠阻尼狀態。自由回響為衰減振盪過程。對應的相軌跡是一簇收斂的對數螺旋線，相應的奇點稱為穩定的焦點口

③當ξ=0時，λ₁，λ₂為一對共扼純虛根，系統的自由回響是簡諧運動，相軌跡是一簇同心橢圓，稱這種奇點為中心點。

④當-1<ξ <0時，λ₁，λ₂為一對具有正實部的共扼復根，系統的自由回響振盪發散。對應的相軌跡是發散的對數螺旋線。相應奇點稱為不穩定的焦點。

⑤當ξ<一1時，λ₁，λ₂為兩個正實根，系統的自由回響為非周期發散狀態。對應的相軌跡是發散的拋物線簇。相應的奇點稱為不穩定的節點。

⑥若系統極點λ₁，λ₂為兩個符號相反的實根，此時系統的自由回響呈現非周期發散狀態。對應的相軌跡是一簇雙曲線，相應奇點稱為鞍點，是不穩定的平衡點。

當系統至少有一個為零的極點時，很容易解出相軌跡方程由此繪製相平面圖影微海危，可以分析系統的運動特性。

相關內容

標準形式的二階系統的微分方程是

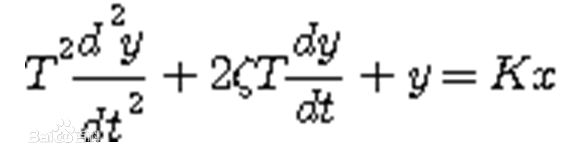
或

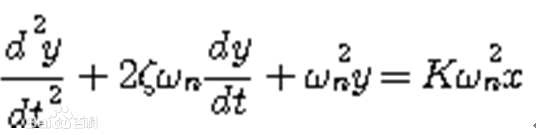
上兩式中，T稱為系統的時間常數。稱為系統的阻尼係數或阻尼比，稱為系統的無阻尼自然振盪頻率或自然頻率。K為放大係數。

標準二階系統的結構圖

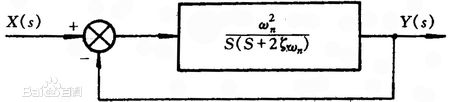
標準形式二階系統的閉環傳遞函式為

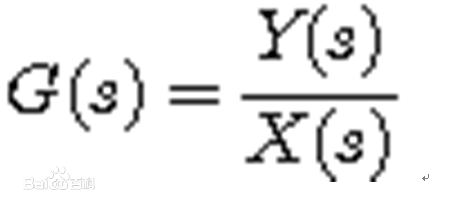
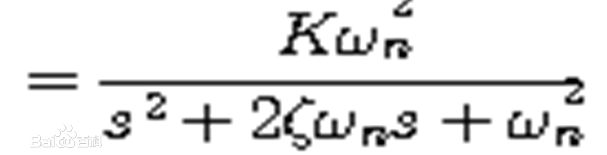
二階系統是控制系統中套用最廣泛、最具代表性的系統。同時，二階系統的分析方法也是分析高階系統的基礎。

單位躍階回響

二階系統的特徵方程為

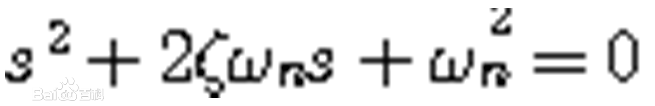
特徵方程的二個根為

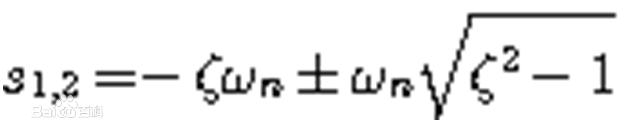
這也是二階系統的閉環極點。
從式可以看出，二階系統的參數，是變化的，取值不同，特徵方程的根（即閉環極點）可能是複數，也可能是實數。系統的回響形式也因此會有較大的區別。
在單位階躍函式輸入下，二階系統的輸出為

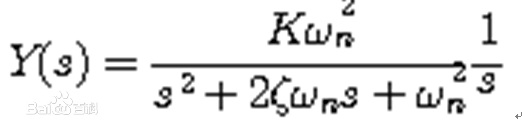
下面分幾種不同的情況來討論二階系統的單位階躍回響。
1.無阻尼狀態
當二階系統的阻尼比等於0時，我們稱二階系統處於無阻尼狀態或無阻尼情況。

2欠阻尼狀態
當二階系統的阻尼係數大於0小於1時，我們稱二階系統的單位階躍回響是欠阻尼情況或者說二階系統處於欠阻尼狀態。

3.臨界阻尼狀態
當阻尼比等於1時，我們稱二階系統處於臨界阻尼狀態或臨界阻尼情況。

4.過阻尼狀態
當阻尼比大於1時,我們稱二階系統處於過阻尼狀態或過阻尼情況。

由描述的二階線性系統自由運動的微分方程

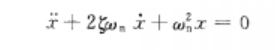
可得

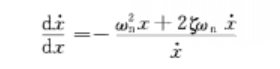
根據式利用等傾斜線法，或者從式解出系統的相軌跡方程，就可以繪製出相應的相平面圖。將不同情形下的二階線性系統相平面圖歸納整理，列在下圖中。

二階線性系統的相軌跡

二階線性系統的相軌跡續表

在式中令x"=x'=0可以得出唯一解x_e=0，這表明線性二階系統的奇點〔或平衡點)就是相平面的原點。根據系統極點在複平面上的位置分布，以及相軌跡的形狀，將奇點分為不同的類型。

①當ξ>=1時，λ₁，λ₂為兩個負實根，系統處於過阻尼(或臨界阻尼)狀態，自由回響按指數衰減。對應的相軌跡是一簇趨向相平面原點的拋物線，相應奇點稱為穩定的節點。

②當0<ξ<1時，λ₁，λ₂為一對具有負實部的共扼復根，系統處於欠阻尼狀態。自由回響為衰減振盪過程。對應的相軌跡是一簇收斂的對數螺旋線，相應的奇點稱為穩定的焦點口

③當ξ=0時，λ₁，λ₂為一對共扼純虛根，系統的自由回響是簡諧運動，相軌跡是一簇同心橢圓，稱這種奇點為中心點。

④當-1<ξ <0時，λ₁，λ₂為一對具有正實部的共扼復根，系統的自由回響振盪發散。對應的相軌跡是發散的對數螺旋線。相應奇點稱為不穩定的焦點。

⑤當ξ<一1時，λ₁，λ₂為兩個正實根，系統的自由回響為非周期發散狀態。對應的相軌跡是發散的拋物線簇。相應的奇點稱為不穩定的節點。

⑥若系統極點λ₁，λ₂為兩個符號相反的實根，此時系統的自由回響呈現非周期發散狀態。對應的相軌跡是一簇雙曲線，相應奇點稱為鞍點，是不穩定的平衡點。

當系統至少有一個為零的極點時，很容易解出相軌跡方程由此繪製相平面圖，可以分析系統的運動特性。

相關內容

標準形式的二階系統的微分方程是

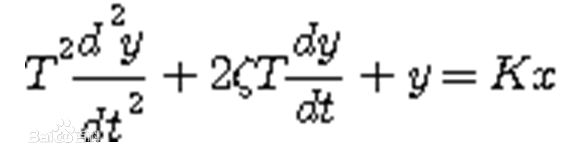
或

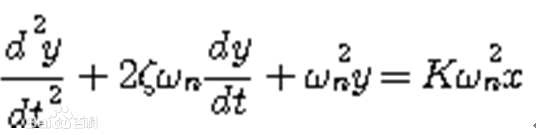
上兩式中，T稱為系統的時間常數。稱為系統的阻尼係數或阻尼比，稱為系統的無阻尼自然振盪頻率或自然頻率。K為放大係數。

標準二階系統的結構圖

標準形式二階系統的閉環傳遞函式為

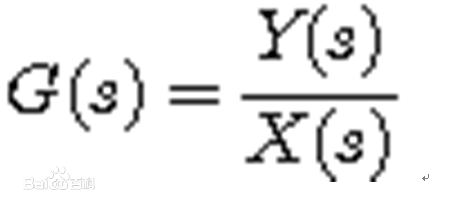
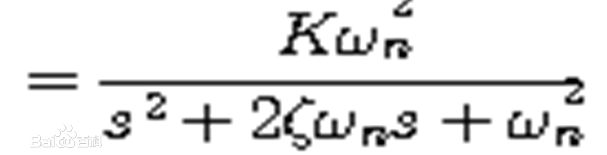
二階系統是控制系統中套用最廣泛、最具代表性的系統。同時，二階系統的分析方法也是分析高階系統的基礎。

單位躍階回響

二階系統的特徵方程為

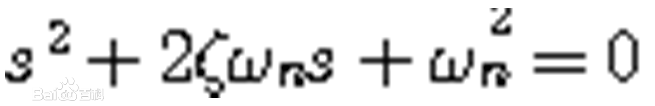
特徵方程的二個根為

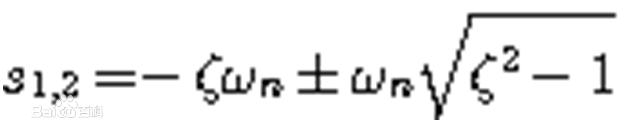
這也是二階系統的閉環極點。
從式可以看出，二階系統的參數，是變化的，取值不同，特徵方程的根（即閉環極點）可能是複數，也可能是實數。系統的回響形式也因此會有較大的區別。
在單位階躍函式輸入下，二階系統的輸出為

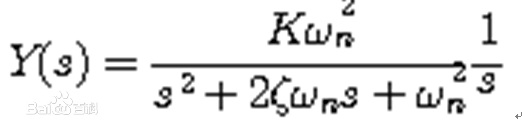
下面分幾種不同的情況來討論二階系統的單位階躍回響。
1.無阻尼狀態
當二階系統的阻尼比等於0時，我們稱二階系統處於無阻尼狀態或無阻尼情況。

2欠阻尼狀態
當二階系統的阻尼係數大於0小於1時，我們稱二階系統的單位階躍回響是欠阻尼情況或者說二階系統處於欠阻尼狀態。

3.臨界阻尼狀態
當阻尼比等於1時，我們稱二階系統處於臨界阻尼狀態或臨界阻尼情況。

4.過阻尼狀態
當阻尼比大於1時,我們稱二階系統處於過阻尼狀態或過阻尼情況。