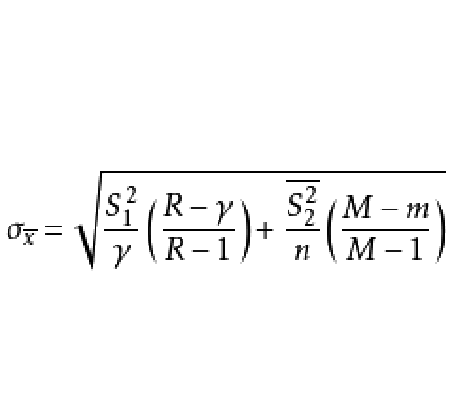二階段抽樣(two-stage sampling)是一種隨機抽樣技術。在規模甚大的總體中(例如在一個省、市中)對居民進行隨機抽樣觀察，為了使樣本較好地反映全省(市)居民的情況，又便於調查工作的組織，可以按居民管轄的行政組織分層，對於二階段抽樣是分成二層，例如第一層是鄉，第二層是村。例如，要調查某縣某病的感染率，第一階段在該縣的各個鄉中隨機抽取若干個鄉，然後以此為基礎在抽出的鄉中進行第二階段抽樣。各隨機抽取若干個村，把抽出的各村居民作為樣本。此種抽樣方法稱為二階段抽樣。
基本介紹
- 中文名：二階段抽樣
- 外文名：two-stage sampling
- 別名：二級隨機抽樣
- 所屬學科：數學（數理統計）
- 相關概念：多階段抽樣，樣本，總體等
二階段抽樣的概念,二階段抽樣標準誤差的測定,實例分析,
二階段抽樣的概念
二階段抽樣也稱二級隨機抽樣，就是在抽取樣本時分兩個階段來進行，第一階段是從總體中用隨機抽樣的方法抽取若干個群體，稱為初級單位。然後在第二階段從這些初級單位中又隨機抽取若干個樣本單位，稱為基本單位或最終單位，最後根據所抽的基本單位組成的樣本進行調查，用取得的樣本資料來推斷總體。如果在二階段抽樣之後，又繼續在被抽中的二階單位中進行第三次、第四次隨機抽樣，就形成了三階抽樣、四階抽樣。二階和二階以上的抽樣都叫做多階抽樣。例如，在農產品產量調查中，由省抽縣，由中選的縣抽鄉，由中選的鄉抽村，由中選的村抽地塊，就是採用多階段抽樣。
多階段抽樣有利於大規模大範圍的抽樣調查的組織與實施，能在一定程度上滿足各級管理部門對調查資料的需求，有利於減少抽樣誤差，提高抽樣估計的精確度。因而，在實際工作中套用較多，如人口、農產品、城鎮居民、農村住戶等調查都可採用這一方法。
二階段抽樣標準誤差的測定
二階段抽樣標準誤差的測定，需要考慮兩個部分的抽樣誤差，一部分是初級單位(群) 之間的差異
和抽取的初級單位的抽樣數目n所決定的抽樣誤差；第二部分是第二階段抽樣的基本單位之間的平均方差
和全部基本單位所決定的抽樣誤差。由於一般採用不重複抽樣，故二階段抽樣標準差測定的基本公式為：
實例分析
某省有100個縣，每縣有200 個村，各村的大小相同。現用兩階段抽樣估計糧食平均畝產，第一階段抽取了A、B、C.D共4 個縣，第二階段從中選縣又各抽取5個村(1，2，3，4，5)，一共為20個樣本村。調查資料整理如表1所示，要求在95%的置信機率下估計全省糧食平均畝產量及置信區間。
A | B | C | D | |
1 | 680 | 620 | 860 | 780 |
2 | 800 | 750 | 810 | 830 |
3 | 780 | 840 | 780 | 850 |
4 | 640 | 760 | 840 | 690 |
5 | 820 | 680 | 680 | 760 |
 | 744.0 | 730 | 794 | 782 |
 | 70.88 | 730 | 794 | 782 |
解： 
總體均值
(千克)
第一階段方差(群間方差)：
平均畝產量的置信區間：
(千克)。
需要指出的是，以上抽樣標準誤差的測定是假定各群、各單位規模大小相同，但在實際抽樣中，各群和各單位的規模大小是不相同的，因此，總體均值的估計、各階段抽樣方差的估計、以及抽樣標準誤差的計算等均應考慮用以加權的方法進行計算。計算公式如下： ．
設：
為總體各群平均單位數；
總體均值估計：
；
抽樣標準誤差：
