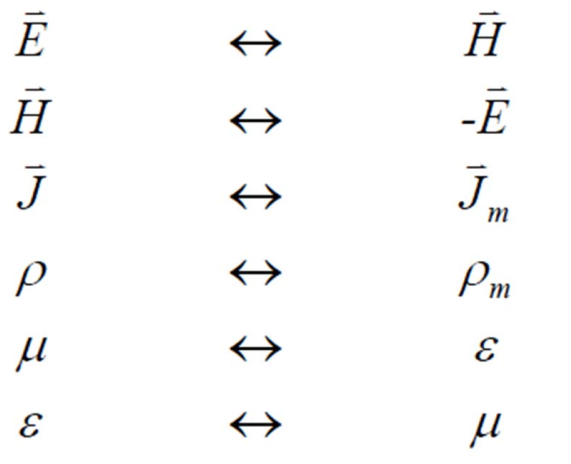如果描述兩種不同物理現象的方程具有相同的數學形式,則它們的解也將具有相同的數學形式,這樣的事實稱為二重性或對偶性。這種具有同樣形式的兩個方程稱為二重性方程或對偶性方程。在二重性方程中占有同樣位置的量稱為二重量或對偶量。
基本介紹
- 中文名:二重性原理
- 別名:對偶原理
- 套用學科:電磁學,工程電動力學
二重性原理詳解
定理推導




因而,在普遍的電磁理論中,激發電磁場的場源應包括電荷、電流、磁荷與磁流。當場源只有電荷與電流時(電流源),由上式可將麥克斯韋方程組表示為下面的形式:




當場源只有磁荷與磁流時(磁流源),同理可將麥克斯韋方程組表示為下面的形式:




我們將只有電流源的麥克斯韋方程組與只有磁流源的麥克斯韋方程組加以比較,可以看出,兩個方程組的數學形式完全相同。如果我們按照下列方式作符號變換:
電流源方程組|磁流源方程組






則可由一個方程組得到另一個方程組。
定理解釋
如果按上述各量的互換關係,可由一類問題的邊界條件(如果只存在電流源的邊界條件)得到另一類問題的邊界條件(如果只存在磁流源的邊界條件),那么由一類問題的解經過上述各量互換後即可得到另一類問題的解,這就是所謂的二重性或對偶性。