在各種數字系統尤其是在數字電子計算機中,用來完成兩個二進制數的大小比較的邏輯電路稱為二進制比較器。在數字電路中,二進制比較器的輸入是要進行比較的兩個二進制數,輸出是比較的結果。
基本介紹
- 中文名:二進制比較器
- 外文名:binary comparator
- 功能:對兩個或多個二進制數進行比較
- 類別:邏輯電路
- 套用:數字系統
- 輸出:二進制數
定義,分類,一位二進制比較器,兩位二進制比較器,集成數值比較器,套用,二進制比較器的位數擴展,三個8位二進制數大小比較電路的實現,
定義
在各種數字系統尤其是在數字電子計算機中,經常需要對兩個二進制數進行大小判別,然後根據判別結果轉向執行某種操作。用來完成兩個二進制數的大小比較的邏輯電路稱為二進制比較器。在數字電路中,二進制比較器的輸入是要進行比較的兩個二進制數,輸出是比較的結果。
分類
二進制比較器就是對兩二進制數A、B進行比較,以判斷其大小的邏輯電路。比較結果有A>B、A<B以及A=B三種情況。根據二進制數位數的不同,二進制比較器主要有一下幾類。
一位二進制比較器
首先討論1位數值比較器。1位數值比較器是多位比較器的基礎。當A和B都是1位二進制數時,它們的取值和比較結果可由1位數值比較器的真值表表示,由真值表可得如下邏輯表達式:

由邏輯表達式可以畫出如圖1所示的邏輯圖。
圖1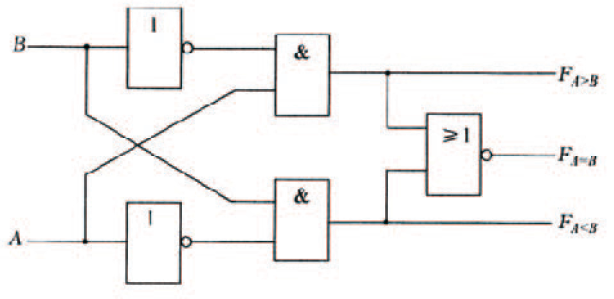

1位數值比較器是多位比較器的基礎。當A和B都是1位數時,它們只能取0或1兩種值,由此可寫出1位數值比較器的真值表如表1:
表1

由以上邏輯表達式可畫出如圖2所示的邏輯電路。實際套用中,可根據具體情況選用邏輯門。
圖2

兩位二進制比較器
現在分析比較兩位數字A1A0和B1B0的情況。 利用1位比較器的結果,可以列出簡化的真值表如表2:
表2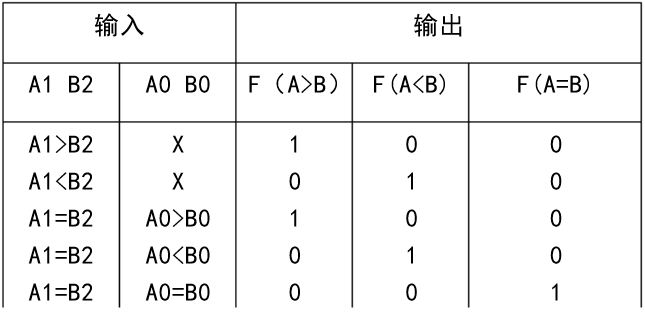

為了減少符號的種類,不再使用字母L,而以(Ai>Bi)、(Ai<Bi)、(Ai=Bi)直接表示邏輯函式。可以由真值表對兩位比較器作如下簡要概述。當高位(A1、B1)不相等時,無需比較低位(A0、B0),兩個數的比較結果就是高位比較的結果。 當高位相等時,兩數的比較結果由低位比較的結果。根據表達式畫出邏輯圖如圖3:
圖3

電路利用了1位數值比較器的輸出作為中間結果。它所依據的原理是,如果兩位數A1A0和B1B0的高位不相等,則高位比較結果就是兩數比較結果,與低位無關。這時,由於中間函式(A1=B1)=0使三個與門G均封鎖,而或門都打開,低位比較結果不能影響或門,高位比較結果則從或門直接輸出。如果高位相等,即(A1=B1)=1,使三個與門均打開,同時由(A1>B1)=0和(A1<B1)=0作用 或門也打開,低位的比較結果直接送達輸出端,即低位的比較結果決定兩數誰大、誰小或者相等。
集成數值比較器
我們以74LS85為例來說明集成數值比較器。集成數值比較器74LS85是4位數值比較器,其功能表如下:
表3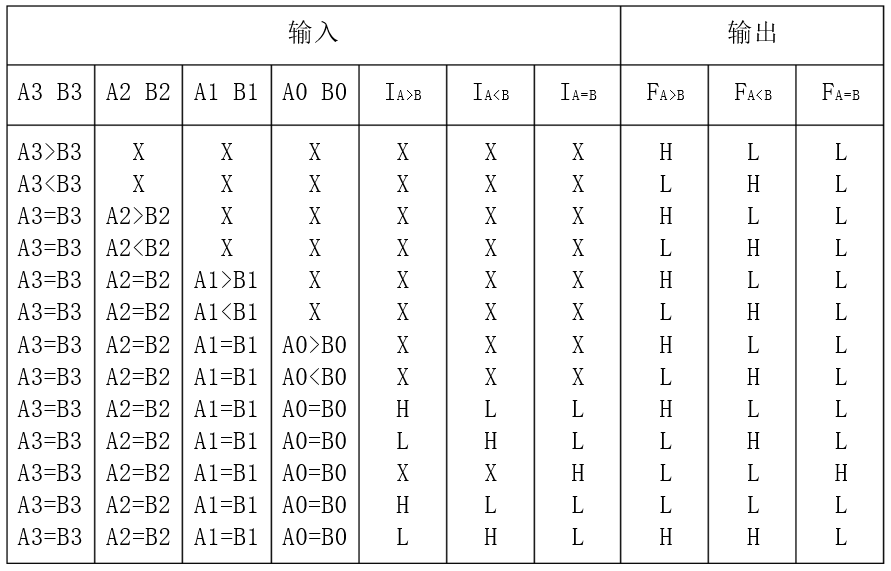

從功能表可以看出,該比較器的比較原理和兩位比較器的比較原理相同。兩個4位數的比較是從A的最高位A3和B的最高位B3進行比較,如果它們不相等,則該位的比較結果可以作為兩數的比較結果。若最高位A3=B3,則再比較次高位A2和B2,余類推。顯然,如果兩數相等,那么,比較步驟必須進行到最低位才能得到結果。 真值表中的輸入變數包括A3與B3、A2與B2、A1與B1、A0與B0和A與B的比較結果。其中A和B是另外兩個低位數,IA>B、IA<B和IA=B是它們的比較結果。設定低位數比較結果輸入端是為了能與其他數值比較器連線,以便組成位數更多的數值比較器。
上式與邏輯圖一致。由上式可以看出,僅對4位數進行比較時,應對IA>B、IAB=IA<B=0,IA=B=1。
套用
二進制比較器的位數擴展
數值比較器的擴展方式有串聯和並聯兩種。下圖表示兩個4位數值比較器串聯而成為一個8位數值比較器。
圖4

我們知道,對於兩個8位數,若高4位相同,它們的大小則由低4位的比較結果確定。因此,低4位的比較結果應作為高4位的條件,即低4位比較器的輸出端應分別與高4位比較器的IA>B、IA<B、IA=B端連線。
三個8位二進制數大小比較電路的實現
由於需要比較三個數(設為C、D、E)的大小,故需要用上面所述的8位比較器三片(用到74LS85共6片),即分別將C、D、E、三個數進行兩兩比較。共得到三組(共9個)輸出端,將三組輸出端組合,輸出結果如下圖:
圖5

寫出每一種輸出結果並綜合比較,共得出如上的19種輸出,由於輸出裡面有很多一樣的結果,(比如:三個輸出分別是C<D、C<E、D<E和三個輸出為C<D、C<E、D=E,這兩種輸出得到的結果都是C最小,E最大),當輸出的結果一樣時可以用一個或門兩在一起,最終共可以得到7種結果。即任意輸入三個8為二進制數,其比較結果只能有7種結果中的一種。

