二維資源分配問題(two dimensional resourcesallocation problem)是一類可用動態規劃方法求解的非線性規劃問題,即把總量各為u和b的某種資源用於生產n種產品的問題。
若把數量為二和y的資源分配於生產第i種產品,其收益為g(二,y),問何分配,才使生產n種產品的總收益最大?其數學模型為
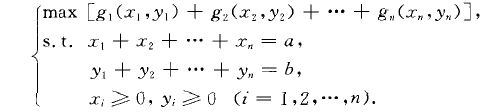
用動態規劃方法來解,則設狀態變數為(二,y),其中二和y分別表示分配用於生產第k種產品至第n種產品的第一種和第二種原料的數量.設決策變數為}xk}yk),二*和yk分別表示分配給第k種產品用的第一種和第二種原料的數量.狀態轉換關係為:i-二一二*,y=y-yk,式中x和y分別表示用來生產第k-}l種產品至第n種產品的第一種和第二種原料的數量.允許決策集合為
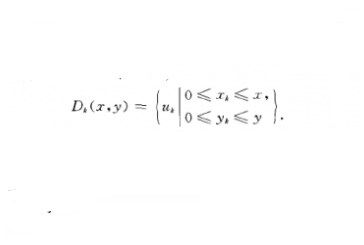
九(二,y)表示以第一種原料數量為x,第二種原料數量為y,分配用於生產第k種產品至第n種產品時所得到的最大收入.由最優性原理(參見“最優性原理”)得
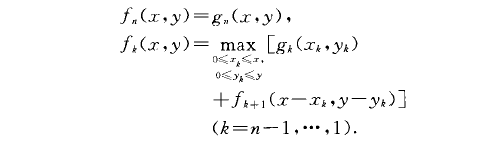
此時,可採用離散化的方法來計算.
