中心位置等距抽樣(centrally located systematic sampling)亦稱“中點定位抽樣(centrically located sampling) ” 、“中點定位機械(或系統)抽樣”。以被抽樣總體中處在中心位置的抽樣單位為起點的機械抽樣。假設被抽樣總體的N個單位按某種順序排列，並依次從1到N編號，處在中心位置的：當N是奇數時為第(N+1)/2個單位，當是偶數時選第N/2或第(N+2)/2個單位。中心定位系統抽樣，即取處在中心位置的單位入樣，並以其為起點向兩個方向上作機械抽樣。可以證明，在一定條件下，這種機械抽樣方法比一般機械抽樣法有更高的精確度。
基本介紹
- 中文名：中心位置等距抽樣
- 外文名：centrally located systematic sampling
- 所屬學科：數學（統計學）
- 別稱：中點定位抽樣、中點定位機械抽樣
- 性質：一種機械抽樣
基本介紹,等距抽樣的含義,等距抽樣的方法,排列方法,抽選步長,抽選方法,等距抽樣的誤差計算,
基本介紹
中心位置等距抽樣亦稱中點定位等距(系統或機械)抽樣，按線性趨勢排列的總體採用直線等距抽樣消除偏倚的一種方法。設總體為N，按大小順序排列，從中抽取容量為n的樣本，抽樣間隔為
，即分割為n段，每段有k個單位。當k為奇數時，取
；當k為偶數時取
或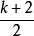
作為起點，樣本依次為
，均為每一段的中點，因而可以防止偏倚。但這種方法一旦排列後，只能抽取一個固定的樣本，失去了隨機抽樣的含義。
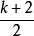
等距抽樣的含義
等距抽樣又稱為機械抽樣或系統抽樣，它是先將總體各單位按有關標誌或無關標誌進行排列，再按照固定的順序和間隔來抽選樣本單位的一種抽樣組織形式。
等距抽樣是不重複抽樣，通常可以保證被抽取的單位在總體中均勻分布，縮小各單位之間的差異程度，提高樣本的代表性。
等距抽樣的方法
等距抽樣時，首先按照一定規則(或根據某個標誌)將抽樣單位依次排列，並隨意確定一個抽樣的“起點”，根據總體容量N和樣本容量n確定抽樣“間隔”——步長h=N/n；然後，以“起點”為第一個抽取的單位，並且每經h個單位抽取一個單位，依此類推。
排列方法
按與調查項目無關或有關的標誌排列樣本，等距抽樣排列方法可分為無關標誌排列和有關標誌排列兩種。例如，按自然出現的順序排列(如自動生產線上源源不斷出現的產品、森林中的樹木、交通幹線上的車輛等)、按姓氏筆畫排列等是無關標誌排列；而家計調查按家庭收入排列、考試調查按學生的考試成績排列等是有關標誌排列。
抽選步長
抽選步長(間隔)h=N/n的選取，應注意兩個方面的問題：排列中可能存在某種“周期性”的變化。例如，一天24小時內高速公路某一地段的流量；商店一周內某一天的銷售額等。在這種情形下，要防止步長與周期相同或為周期的倍數，否則會產生系統偏差。當h=N/n不是自然數時，應採取相應措施加以解決。例如，隨機地刪除一些單位，或採用首尾相連的排列方法及下面介紹的循環抽選法。
抽選方法
保障樣本的代表性，是等距抽樣選擇抽樣起點的原則。常用的等距抽樣法有隨機起點抽樣法、中點定位抽樣法、對稱抽樣法、半步點起點抽樣法、循環等距抽樣法等。下面介紹抽選方法時，符號N表示總體容量，n表示樣本容量，h表示抽樣步長。
(1) 隨機起點等距抽樣法 隨機起點抽樣法是在依次排列的前h個單位中隨機抽取一個單位入樣，假設第一個入樣的單位的編號為k(1≤k≤n)，那么第j(j=2,3,...,n)次抽樣抽選第k+(j-1)h個單位的樣本人樣。需要注意的是，這種方法不宜用於抽樣單位按有關標誌排列的情形，因為在這種情況下可能產生系統誤差。
(2)中點定位等距抽樣法 在N個抽樣單位排列中，選位於中點的單位做抽樣起點的一種等距抽樣方法。
(3)對稱等距抽樣法 首先依次排列在前面的h個抽樣單位中，隨機抽取一個做起點，假設其編號為k(1≤k≤h)；然後依次抽選第2h-k，2h+k，4h-+k，4h+k，6h-k，6h+k……個單位人樣(見圖1)。
圖1 對稱等距抽樣法示意圖(4)半步長起點等距插樣法 先將總體全部N個單位的排列分為長為h的n段，抽選位於各段中點的單位入樣。這種等距抽樣法在實踐中得到廣泛套用，通常都能取得滿意的結果。其局限性在於，不能嚴格遵循隨機原則，並且無法進行樣本輪換。
(5)循環等距抽樣法 首先按一定規則或某個標誌，將總體全部N個單位排成首尾相連的圓形，設h為最接近N/n的自然數，而k是在前h個數中任意一個自然數；以第k個單位做起點、以h為步長，一個單位一個單位地抽取直到抽夠n個單位為止。
等距抽樣的誤差計算
直接計算等距抽樣的平均誤差比較困難。通常是用簡單隨機抽樣的誤差公式來計算按無關標誌排列的等距抽樣的平均誤差；用分層抽樣的誤差公式來計算有關標誌排列的等距抽樣的平均誤差。
