不動環,((fixed ring)由不動域引申的概念.
若群G作用於環R為R的自同構,"r表示rER在g作用下的像,則稱R的子環
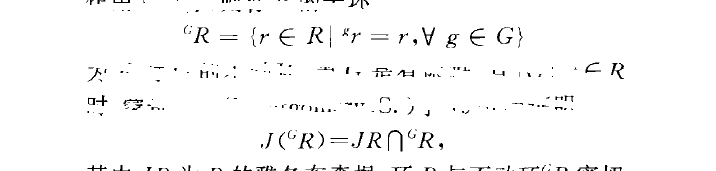
為R對G的不動環.當G是有限群,且!GI一‘ER時,蒙哥馬利(Montgomery,S.)於1976年證明:
I (`'R) -JR自`'R,
其中,IR為R的雅各布森根.環R與不動環“R密切相關,若R無一GI扭且R是半素環,則‘浪也是半素環;若R是有1單環,G作用是外自同構,則‘浪是本原環;若R是半單阿廷環,且一G}一‘ER,則“R也是半單阿廷環.不動環對建立環上伽羅瓦理論起關鍵作用.除環、本原環、素環、半素環上的伽羅瓦理論己分別由蒙哥馬利、帕斯曼(Passman,D. S.)和卡爾欽哥(Kharchenko, V. K.)建立.
