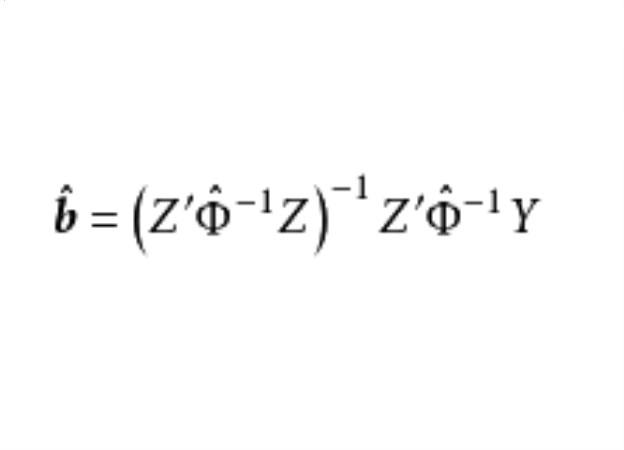三階段最小二乘法是聯立方程模型的一種完全信息估計方法,簡稱3SLS方法。所謂“完全信息估計法”指利用所有可用的信息,同時估計模型中的所有方程。本法基本思想是:套用兩階段最小二乘法的估計誤差構造模型隨機擾動項協方差矩陣的統計量,從而對整個模型進行廣義最小二乘估計。本法由塞拉和希爾於1962年提出。套用本法的主要步驟為:(1)模型系統要求可識別,抽去所有的定義方程式(即恆等式);(2)對模型簡化式作最小二乘估計;(3)以上述估計量為工具變數對模型結構式進行最小二乘估計(即兩階段最小二乘估計),並計算估計誤差;(4)以兩階段估計誤差構造擾動項方差的統計量,進行廣義最小二乘估計。本法估計結果,在一定條件下比兩階段最小二乘估計具有更好的漸近有效性。
基本介紹
- 中文名:三階段最小二乘法
- 簡稱:3SLS方法
- 所屬學科:數理科學
- 提出者:泰爾(Theil)和澤爾納(Zellner)
- 提出時間:1962年
三階段最小二乘法的基本思想,三階段最小二乘法的步驟,3SLS估計量的特性,
三階段最小二乘法的基本思想
三階段最小二乘法是泰爾(Theil)和澤爾納(Zellner)在1962年提出的一種完全信息方法。它是2SLS法的邏輯推廣。
將2SLS法推廣到3SLS法,基於以下兩個想法:
(1)2SLS只使用了模型的一部分信息,忽視了模型結構對其他方程的參數值所施加的全部約束條件。
(2)忽視了模型各個方程隨機擾動項的同期相關性,即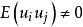 ,其中i指第i個方程,j指第j個方程。
,其中i指第i個方程,j指第j個方程。
這樣,單一方程估計法就不會很有效,故有改進的必要。改進的方法是引進廣義最小二乘法。因此,三階段最小二乘法的第一、二階段是兩階段最小二乘法,第三階段是廣義最小二乘法的套用。三階段最小二乘法要比二階段最小二乘法具有更好的漸進有效性。但是,三階段最小二乘法計算很複雜,樣本容量必須足夠大。
三階段最小二乘法的步驟
設模型中包括G個內生變數和K個前定變數,其第i個方程表示為:

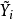
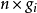
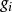
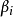


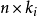
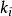
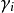

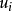
方程(1)的矩陣形式:
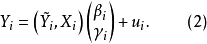
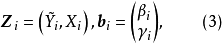
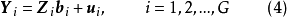
第一階段,把模型(1)化為約簡型:
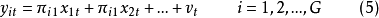
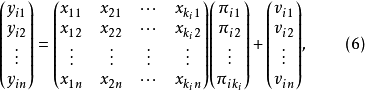

對(7)的每一個方程套用OLS法,求得 的估計量
的估計量 。
。

第二階段,把 代入結構方程(4)右邊,對變換了的方程套用OLS法,求得
代入結構方程(4)右邊,對變換了的方程套用OLS法,求得 的2SLS估計值,並用來估計各方程中隨機擾動項
的2SLS估計值,並用來估計各方程中隨機擾動項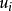 ,得隨機擾動項的估計值
,得隨機擾動項的估計值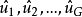 。注意這裡
。注意這裡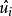 是(n×1)列向量。
是(n×1)列向量。

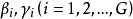
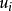
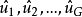
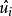
第三階段:
我們已經知道X為所有前定變數的觀測值(n×k)階矩陣,用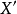 左乘方程(4),得到KG個方程的方程組:
左乘方程(4),得到KG個方程的方程組:
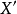
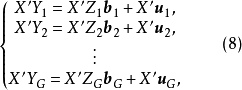
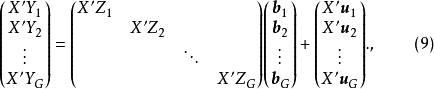
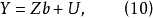
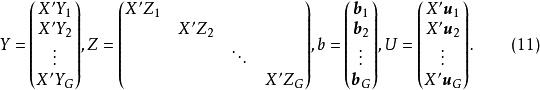
顯然合成擾動隨機項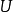 ,是隨著矩陣
,是隨著矩陣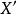 一起變化的,因而具有異方差性,為此需要套用廣義最小二乘法(GLS),但是,廣義最小二乘法的計算需要知道
一起變化的,因而具有異方差性,為此需要套用廣義最小二乘法(GLS),但是,廣義最小二乘法的計算需要知道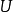 的協方差陣。
的協方差陣。
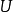
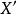
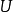
下面我們先解決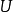 的協方差陣的計算:
的協方差陣的計算:
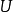
每一個方程都有n個觀測值。記第i個方程與第j個方程同期隨機擾動項的協方差為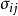 ,並假定不同期隨機擾動項不相關。原模型
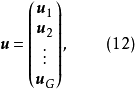
,並假定不同期隨機擾動項不相關。原模型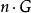 個隨機擾動項可用矩陣定義為
個隨機擾動項可用矩陣定義為
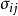
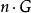
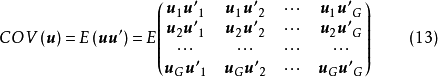
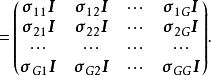
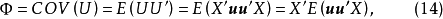
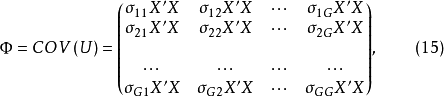

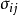


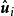
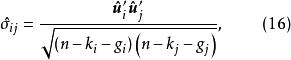

3SLS估計量的特性
3SLS估計量的特性是:
(1)3SLS估計量是非無偏,但是一致估計量。
(2)3SLS估計量比2SLS估計量更有效,因為在計估過程中使用的信息比2SLS法多。
3SLS法作為一種系統估計法,其主要困難是參數估計值容易受到模型中個別方程定型偏倚的影響。也就是說,只要有一個方程因制定不當而發生偏誤,這種偏誤將通過整體性的估計方法傳遞給整個模型中的每一個參數,使全部參數估計值發生變化。因此在實際套用這種方法時應注意以下條件:
(1)模型的每一個方程都是正確制定的,而且都是可識別的。
(2)原模型中隨機擾動項滿足經典假定;並且不同方程不同期之間隨機擾動項不相關;
(3)從聯立方程中去掉任何定義方程(或恆等式);
(4)從聯立方程中去掉不能識別的方程;
(5)如果 是分塊對角陣,那么3SLS可以分別用於對應每塊的方程組。
是分塊對角陣,那么3SLS可以分別用於對應每塊的方程組。